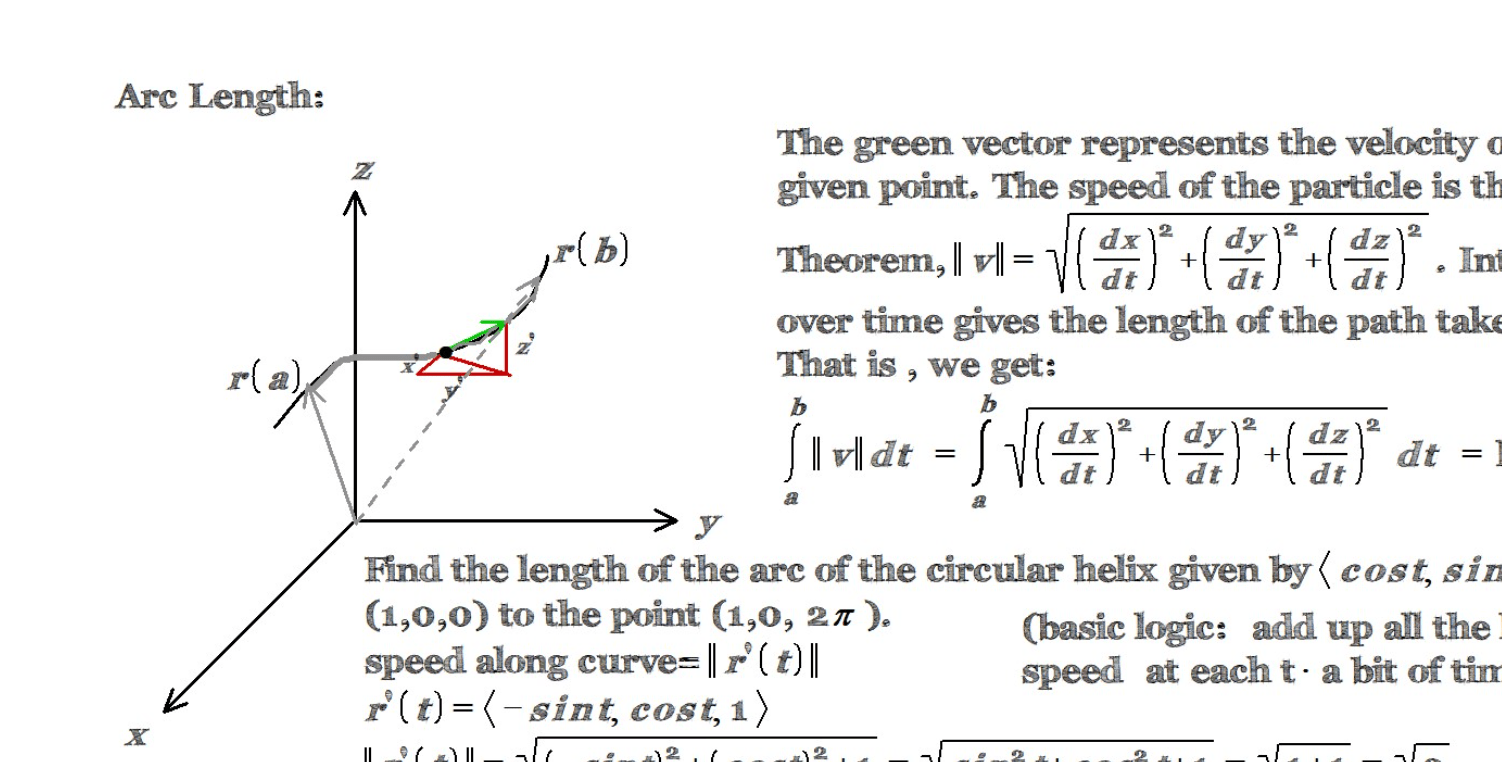
Formula for Arc Length of a 3D Curve
The arc length of a 3D curve defined by a vector-valued function r(t) = (x(t), y(t), z(t)) in the interval [a, b] can be calculated using the following formula:
Arc Length = ∫ab √((dx/dt)^2 + (dy/dt)^2 + (dz/dt)^2) dt
Where:
- (dx/dt), (dy/dt), (dz/dt) are the derivatives of x(t), y(t), z(t) with respect to t.
- [a, b] is the interval over which the curve is defined.
This formula calculates the length of the curve in 3D space by integrating the square root of the sum of the squares of the derivatives of the component functions.
It’s important to parameterize the curve properly and calculate the derivatives correctly before applying the formula.