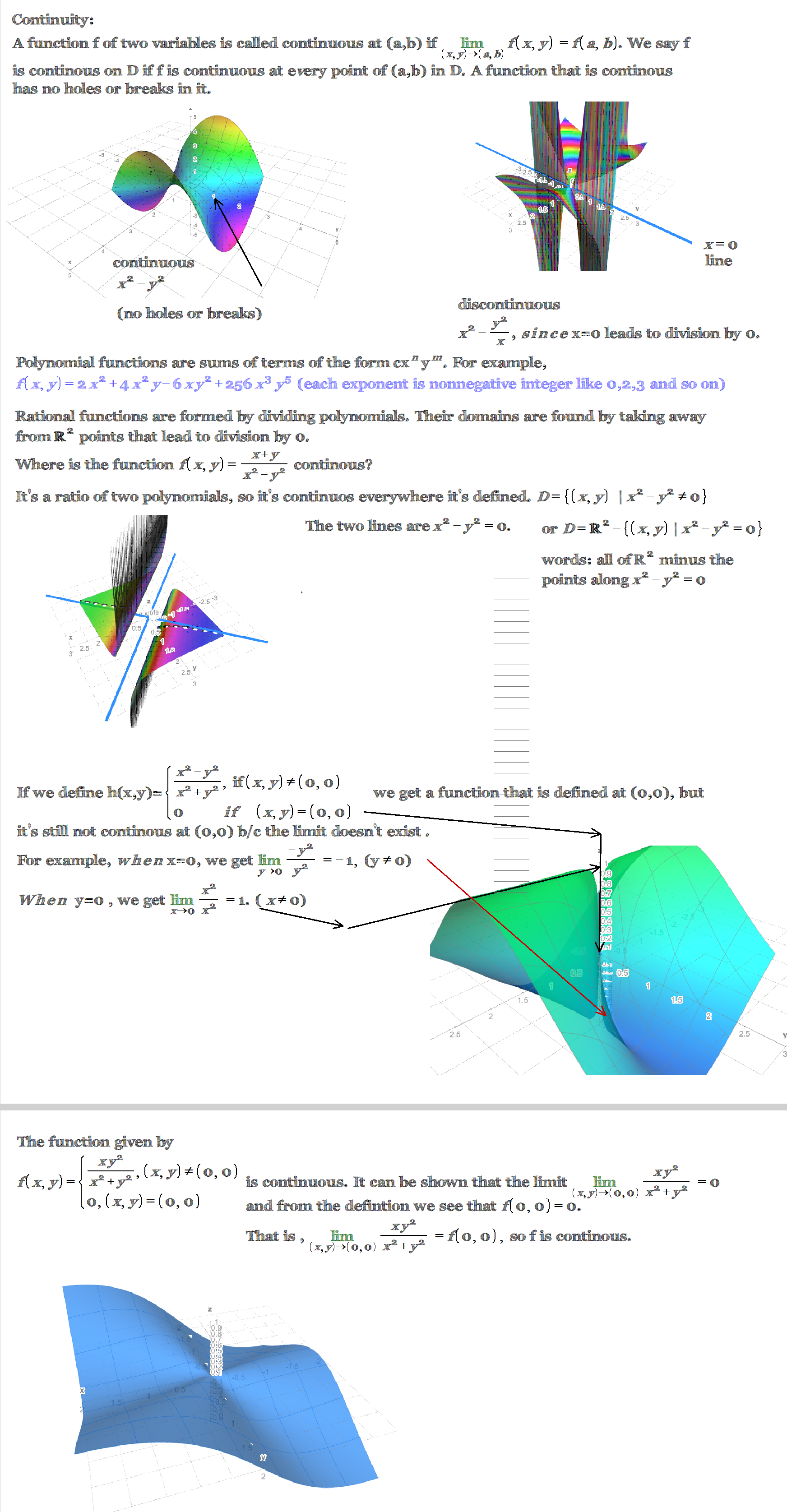
It shows a summary of the continuity of functions of two variables.
The first part of the image defines continuity at a point for a function of two variables. A function f(x, y) is continuous at (a, b) if and only if lim(x, y) → (a, b) f(x, y) = f(a, b).
The second part of the image shows some examples of continuous and discontinuous functions. The continuous functions are the polynomial function and the rational function whose denominator is not 0 at (0, 0). The discontinuous function is the rational function whose denominator is 0 at (0, 0).
The third part of the image discusses the continuity of a function on a domain. A function f(x, y) is continuous on a domain D if and only if it is continuous at every point in D.
The fourth part of the image discusses the continuity of a rational function. A rational function is continuous on a domain D if and only if the denominator is not 0 at any point in D.
The fifth part of the image discusses the continuity of a function that is defined piecewise. A function that is defined piecewise is continuous at a point if and only if the two pieces of the function are continuous at the point.
I hope this explanation is clear. Let me know if you have any other questions.