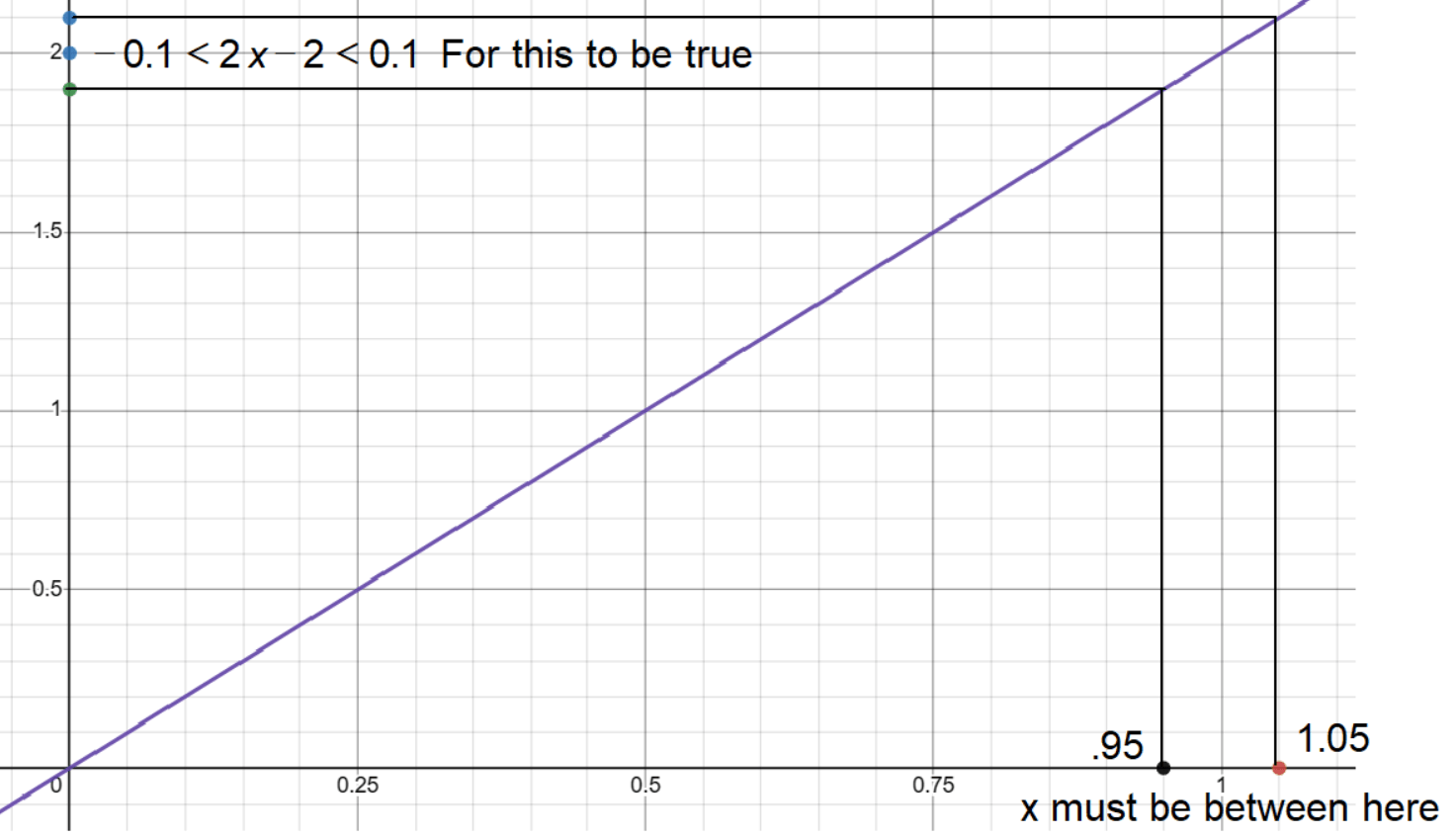
Finding the Range of x for f(x) = 2x to be within 0.1 of 2
Objective: Our goal is to find the range of x values where the function f(x) = 2x is within 0.1 units of the value 2.
Step 1: Set Up the Inequality
We start with the inequality |2x – 2| < 0.1 to represent that f(x) should be within 0.1 of 2.
Step 2: Remove the Absolute Value
We rewrite the inequality without the absolute value as -0.1 < 2x - 2 < 0.1.
Step 3: Simplify the Inequality
We add 2 to all three sides of the inequality to isolate 2x. This gives us -0.1 + 2 < 2x < 0.1 + 2, which simplifies to 1.9 < 2x < 2.1.
Step 4: Divide by 2
We divide all terms by 2 to solve for x. This gives us 0.95 < x < 1.05.
Conclusion: The x values must lie between 0.95 and 1.05 for f(x) = 2x to be within 0.1 of 2.
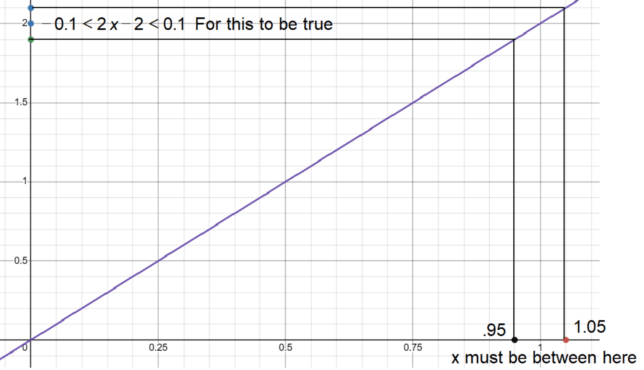
Calculus Context for Finding the Range of x for f(x) = 2x to be within 0.1 of 2
Limits: This type of question is closely related to the concept of limits in calculus. Essentially, we are interested in the limit of f(x) as x approaches 1. We want to find an interval around x = 1 where f(x) is close to f(1), which is 2.
Continuity: The question also touches on the concept of continuity. If a function is continuous at a point, it means that we can find an interval around that point where the function’s value remains close to the value at that point. In this case, f(x) = 2x is a continuous function.
Linear Approximation: The function f(x) = 2x is linear, making it its own best linear approximation. For more complex functions, you might use the tangent line at a point to approximate the function near that point.
Approximations: This question is essentially asking for an approximation of the function value near a specific point. In calculus, approximations are often used to understand the behavior of functions near specific points, especially when exact values are difficult to find.
Finding the Range of x for f(x) = 2x to be within a of 2
Objective: We aim to find the values of x where the function f(x) = 2x is within a units of the value 2.
Step 1: Set Up the Inequality
We start by setting up an inequality that captures the condition “within a of 2”. The inequality is |2x – 2| < a.
Step 2: Simplify the Inequality
We can simplify the inequality by dividing each term by 2. This gives us |x – 1| < a/2.
Step 3: Solve the Inequality
We can now rewrite this as two separate inequalities without breaking the absolute value: -a/2 < x - 1 < a/2.
Adding 1 to each term, we get 1 – a/2 < x < 1 + a/2.
Conclusion: The values of x must be between 1 – a/2 and 1 + a/2 for f(x) = 2x to be within a of 2.
Finding the Range of x for f(x) = 2x to be within 0.1 of L
Objective: We aim to find the values of x where the function f(x) = 2x is within 0.1 units of a given value L.
Step 1: Set Up the Inequality
We start by setting up an inequality that captures the condition “within 0.1 of L”. The inequality is |2x – L| < 0.1.
Step 2: Simplify the Inequality
We can simplify the inequality by dividing each term by 2. This gives us |x – L/2| < 0.05.
Step 3: Solve the Inequality
We can now rewrite this as two separate inequalities without breaking the absolute value: -0.05 < x - L/2 < 0.05.
Adding L/2 to each term, we get L/2 – 0.05 < x < L/2 + 0.05.
Conclusion: The values of x must be between L/2 – 0.05 and L/2 + 0.05 for f(x) = 2x to be within 0.1 of L.
Finding the Range of x for f(x) = 2x to be within a of L
Objective: We aim to find the values of x where the function f(x) = 2x is within a units of a given value L, where L is f(x).
Step 1: Set Up the Inequality
We start by setting up an inequality that captures the condition “within a of L”. The inequality is |2x – L| < a.
Step 2: Simplify the Inequality
We can simplify the inequality by dividing each term by 2. This gives us |x – L/2| < a/2.
Step 3: Solve the Inequality
We can now rewrite this as two separate inequalities without breaking the absolute value: -a/2 < x - L/2 < a/2.
Adding L/2 to each term, we get L/2 – a/2 < x < L/2 + a/2.
Conclusion: The values of x must be between L/2 – a/2 and L/2 + a/2 for f(x) = 2x to be within a of L.