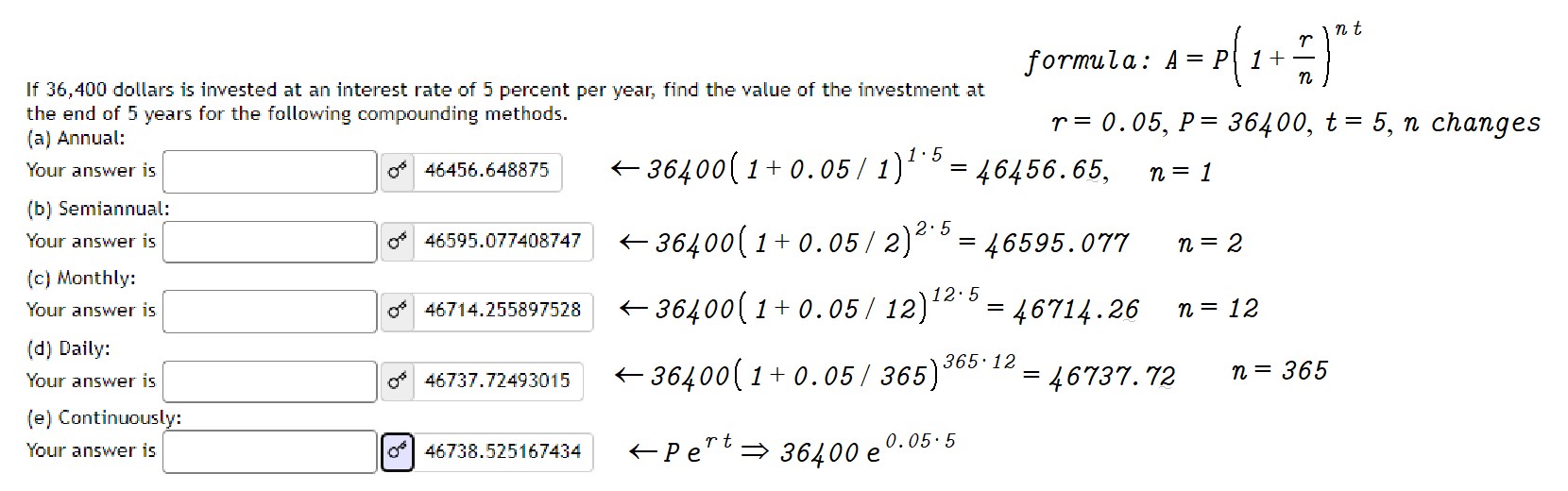Derivation of the Discrete Compounding Formula
| \( A = P \) | Start with the initial amount of money invested or borrowed, known as the principal (P). |
| \( \frac{r}{n} \) | If interest is compounded \( n \) times per year, divide the annual interest rate (r) by the number of compounding periods per year (n) to find the interest rate for one compounding period. |
| \( \frac{r}{n}P \) | Multiply the interest rate for one compounding period by the principal (P) to find the interest earned for one period. |
| \( A = P\left(1 + \frac{r}{n}\right) \) | Add the interest earned for one period to the principal to find the total amount after one compounding period. |
| \( A = P\left(1 + \frac{r}{n}\right)^n \) | Repeat this process for \( n \) compounding periods in one year, representing the multiplication of \( \left(1 + \frac{r}{n}\right) \) by itself \( n \) times. |
| \( A = P\left(1 + \frac{r}{n}\right)^{nt} \) | Repeat the compounding process for \( t \) years, equivalent to multiplying the expression for one year, \( P\left(1 + \frac{r}{n}\right)^n \), by itself \( t \) times. The exponent \( nt \) represents the total number of compounding periods over \( t \) years. |
Summary: The formula \( A = P\left(1 + \frac{r}{n}\right)^{nt} \) calculates the future value with compounded interest, considering the principal (P), annual interest rate (r), number of compounding periods per year (n), and number of years (t).
discrete compounding sample calculations, continuous compounding included.