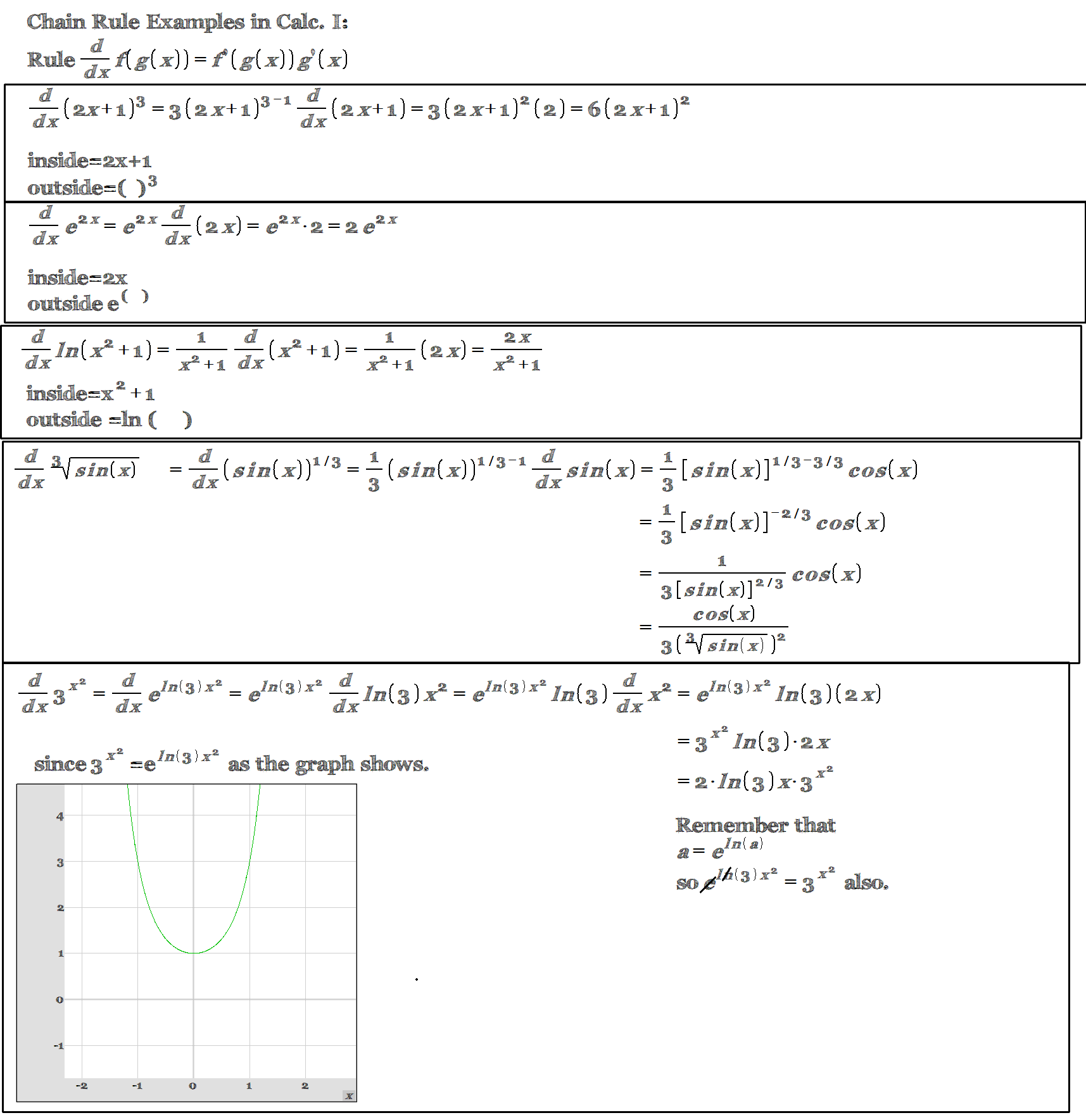
Chain Rule Examples in Calculus
The image you sent me contains a table of chain rule examples in calculus. The table shows how to use the chain rule to find the derivative of a composite function.
Chain Rule Formula:
The chain rule states that the derivative of f(g(x)) is f'(g(x))g'(x). In other words, the derivative of a composite function is the product of the derivative of the outer function and the derivative of the inner function.
Examples:
The table in the image shows several examples of how to use the chain rule. For example, the first example shows how to find the derivative of (2x+1)³. The outer function in this case is the cube function, and the inner function is 2x+1. The derivative of the cube function is 3(x+1)², and the derivative of 2x+1 is 2. So, the derivative of (2x+1)³ is 3(2x+1)² * 2 = 6(2x+1)².
The other examples in the table follow the same pattern. The outer function is the one that is applied first, and the inner function is the one that is applied second. The derivative of the outer function is multiplied by the derivative of the inner function to find the derivative of the composite function.