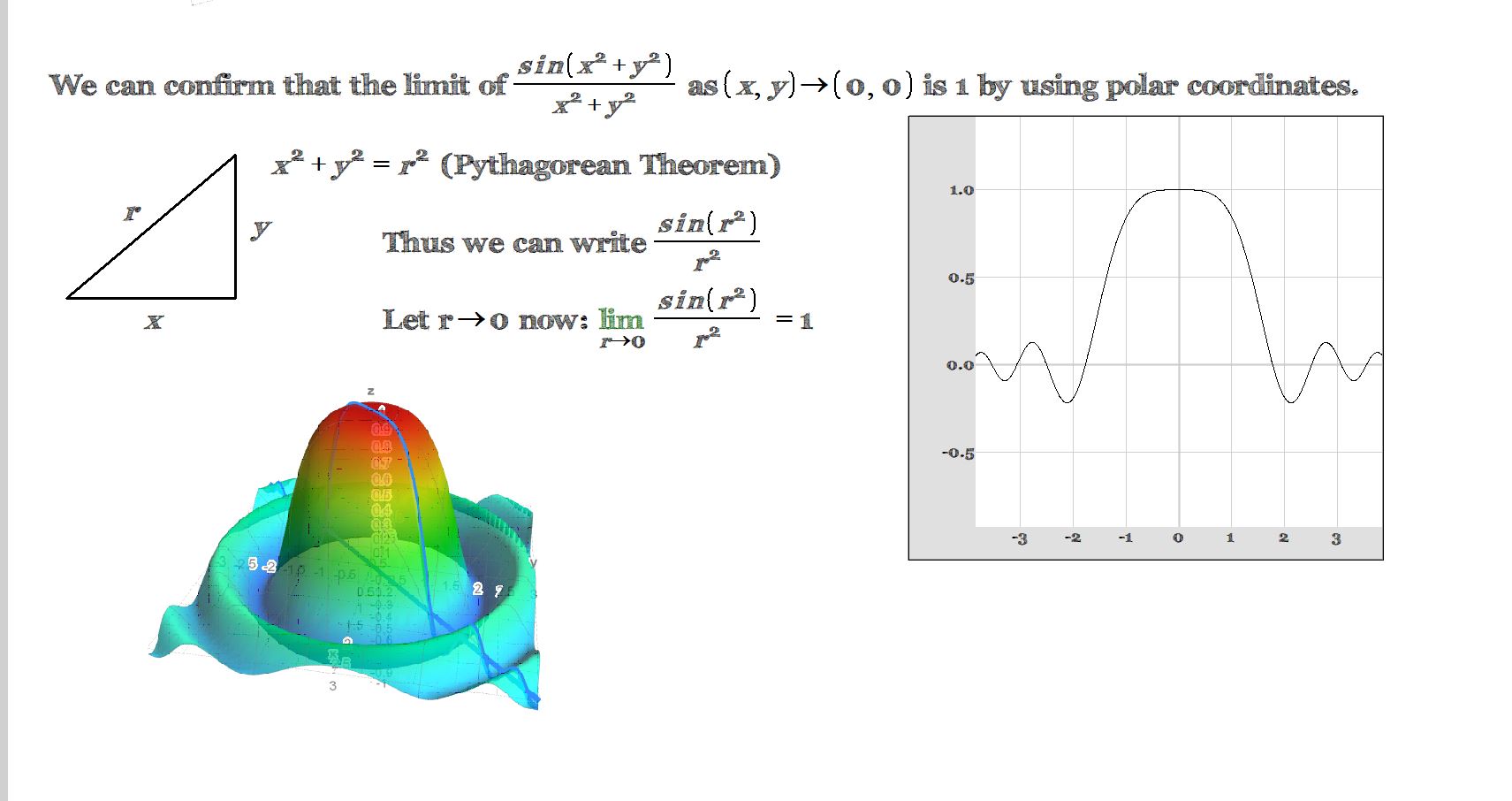
Limit of sin(x²+y²)/(x²+y²) as (x,y) → (0,0) Using Polar Coordinates
The document shows how to find the limit of sin(x²+y²)/(x²+y²) as (x,y) approaches (0,0) using polar coordinates. In polar coordinates, (x,y) is represented by the point (r,θ), where r is the distance from the origin and θ is the angle between the positive x-axis and the line segment connecting the origin to (x,y).
Step 1: Convert to Polar Coordinates
The first step is to convert the rectangular coordinates (x,y) to polar coordinates. In polar coordinates, x = r cos θ and y = r sin θ.
Step 2: Substitute into the Expression
After converting to polar coordinates, the expression sin(x²+y²)/(x²+y²) becomes sin(r²)/(r²).
Step 3: Evaluate the Limit
The document then shows how to evaluate the limit of this expression as (r,θ) approaches (0,0).
I hope this summary is helpful. Let me know if you have any other questions.