---

---

Finding When Wade’s Age Was Three Times Heather’s Age

Introduction:

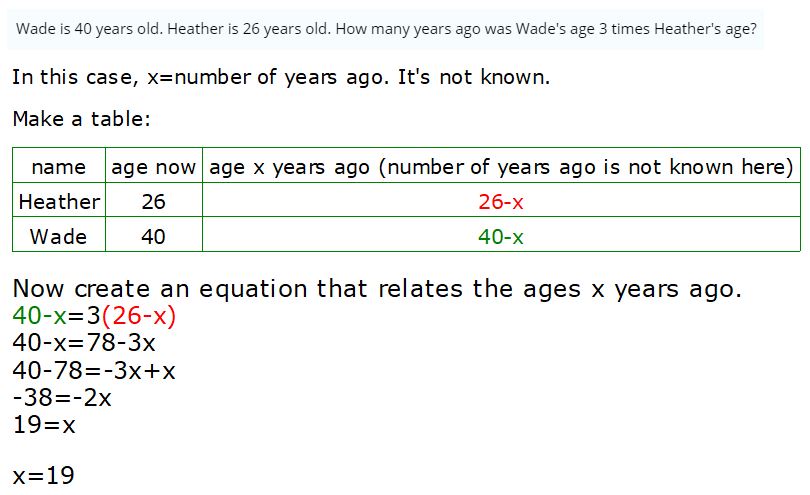
We are given that Wade is currently 40 years old and Heather is 26 years old. We are tasked with finding out how many years ago Wade’s age was three times Heather’s age.

Step 1: Define the Variables

Let’s use W to represent Wade’s current age, which is 40, and H for Heather’s current age, which is 26. We’ll use Y to represent the number of years ago when Wade’s age was three times Heather’s age.

Step 2: Translate the Problem into a Mathematical Equation

The condition we need to find is when Wade’s age was three times Heather’s age. To represent their ages Y years ago, we subtract Y from their current ages. Wade’s age Y years ago becomes W – Y, and Heather’s becomes H – Y. This condition can be translated into the equation: W – Y = 3(H – Y).

Step 3: Substitute the Known Values

We know that W = 40 and H = 26. Substituting these into the equation, we get: 40 – Y = 3(26 – Y).

Step 4: Solve the Equation

Expand the equation: 40 – Y = 78 – 3Y.

Rearrange to isolate Y: 2Y = 38.

Solve for Y: Y = 19.

Conclusion:

19 years ago, Wade’s age was three times Heather’s age.