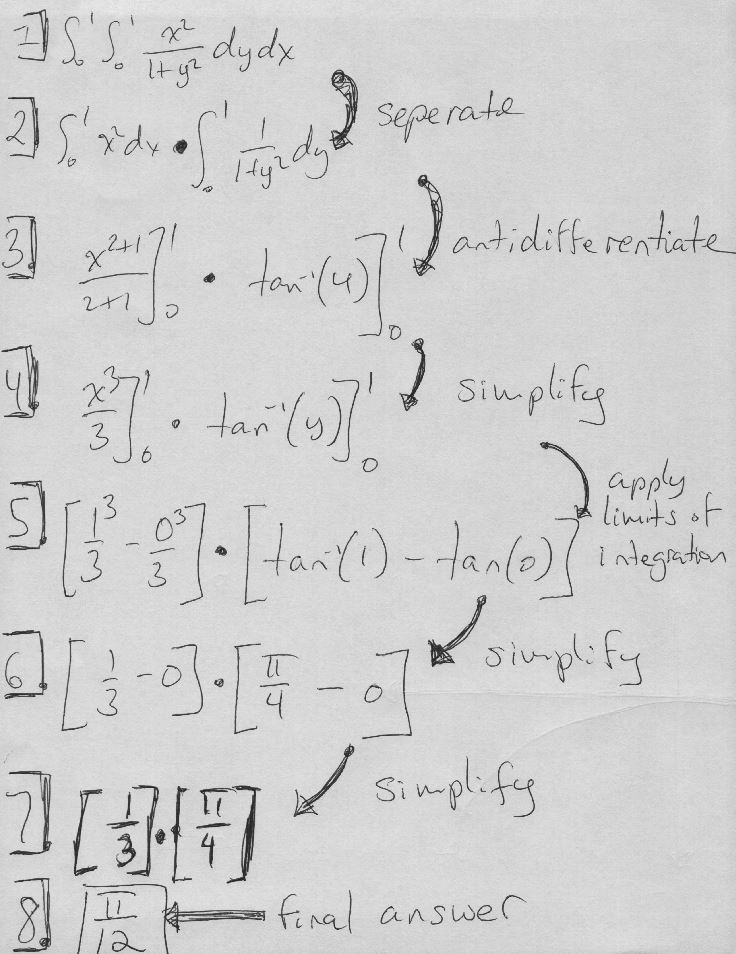
Double Integral Evaluation

We aim to evaluate the following double integral:

∫₀¹ ∫₀¹ (x² / (1 + y²)) dy dx

Step 1: Integrate with respect to \( y \)

Firstly, we focus on integrating the inner integral with respect to \( y \), treating \( x \) as a constant:

∫₀¹ (x² / (1 + y²)) dy

This simplifies to:

x² ∫₀¹ (1 / (1 + y²)) dy

The integral of \( 1 / (1 + y²) \) is \( tan⁻¹(y) \). Therefore, the result becomes:

x² [tan⁻¹(y)]₀¹ = x² (tan⁻¹(1) – tan⁻¹(0)) = x² (π/4 – 0) = πx²/4

Step 2: Integrate with respect to \( x \)

Next, we integrate the resulting expression with respect to \( x \):

∫₀¹ (πx² / 4) dx

Applying the power rule for integration, we get:

π/4 ∫₀¹ x² dx = π/4 [x³/3]₀¹ = π/4 (1/3 – 0) = π/12

Final Result

The value of the double integral is \( \frac{\pi}{12} \).

Simple Example of Double Integral Evaluation

We aim to evaluate the following double integral:

∫₀¹ ∫₀¹ x²y dy dx

Step 1: Integrate with respect to \( y \)

First, we focus on the inner integral, which is with respect to \( y \):

∫₀¹ x²y dy

This simplifies to:

x² ∫₀¹ y dy = x² [y²/2]₀¹ = x² (1/2 – 0) = x²/2

Step 2: Integrate with respect to \( x \)

Next, we integrate the resulting expression with respect to \( x \):

∫₀¹ x²/2 dx

Applying the power rule for integration, we get:

1/2 ∫₀¹ x² dx = 1/2 [x³/3]₀¹ = 1/2 (1/3 – 0) = 1/6

Final Result

The value of the double integral is \( 1/6 \).