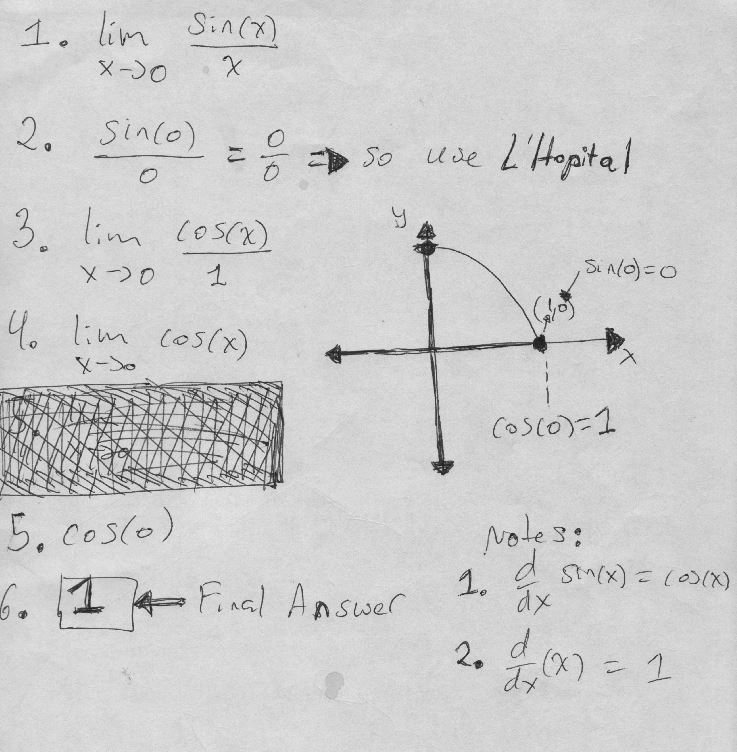
Limit of sin(x)/x as x approaches 0 using L’Hôpital’s Rule

We aim to find the limit of sin(x)/x as x approaches 0. This is a classic limit problem in calculus, and we’ll use L’Hôpital’s Rule to solve it.

Step 1: Check Indeterminate Form

First, we check if the function sin(x)/x is in an indeterminate form \( \frac{0}{0} \) as \( x \) approaches 0. Indeed, \( \sin(0) = 0 \) and \( x = 0 \), so we have \( \frac{0}{0} \).

Step 2: Differentiate the Numerator and Denominator

Next, we differentiate both the numerator and the denominator with respect to \( x \).

\( f'(x) = \cos(x) \) and \( g'(x) = 1 \)

Step 3: Apply L’Hôpital’s Rule

Now, we apply L’Hôpital’s Rule, which gives us:

\( \lim_{{x \to 0}} \frac{\sin(x)}{x} = \lim_{{x \to 0}} \frac{\cos(x)}{1} \)

Step 4: Evaluate the Limit

Finally, we evaluate \( \lim_{{x \to 0}} \frac{\cos(x)}{1} \), which is \( \cos(0) = 1 \).

Final Result

The limit of \( \frac{\sin(x)}{x} \) as \( x \) approaches 0 is 1. This result is obtained using L’Hôpital’s Rule, which allows us to differentiate the numerator and the denominator to find the limit.