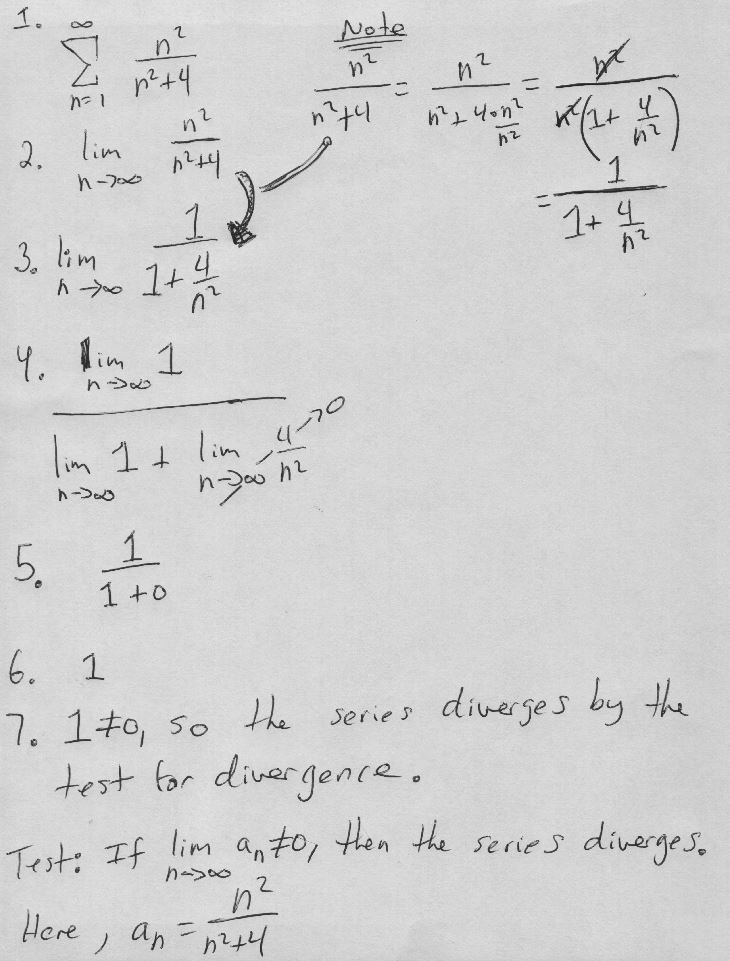
Convergence or Divergence of \(\sum_{n=1}^{\infty} \frac{n^2}{n^2 + 4}\)

This guide explains how to determine if the mathematical series \(\sum_{n=1}^{\infty} \frac{n^2}{n^2 + 4}\) converges or diverges using the Limit Test.

Step 1: Identify the Term

The term we’re interested in is \( a_n = \frac{n^2}{n^2 + 4} \). This is the term given in the series we’re testing.

Step 2: Calculate the Limit

We need to find the limit of \( a_n \) as \( n \) approaches infinity. This is a requirement of the Limit Test.

Output: \(\lim_{{n \to \infty}} \frac{n^2}{n^2 + 4}\)

Step 3: Solve the Limit

As \( n \) approaches infinity, the \( +4 \) in the denominator becomes negligible. Therefore, the limit is \( 1 \), which is not equal to zero.

Output: \(\lim_{{n \to \infty}} \frac{n^2}{n^2 + 4} = 1\)

Step 4: Apply the Limit Test

Since the limit is \( 1 \), which is not zero, the series diverges according to the Limit Test.

Output: The series \(\sum_{n=1}^{\infty} \frac{n^2}{n^2 + 4}\) diverges.

Conclusion

By using the Limit Test, we can conclude that the series \(\sum_{n=1}^{\infty} \frac{n^2}{n^2 + 4}\) diverges.