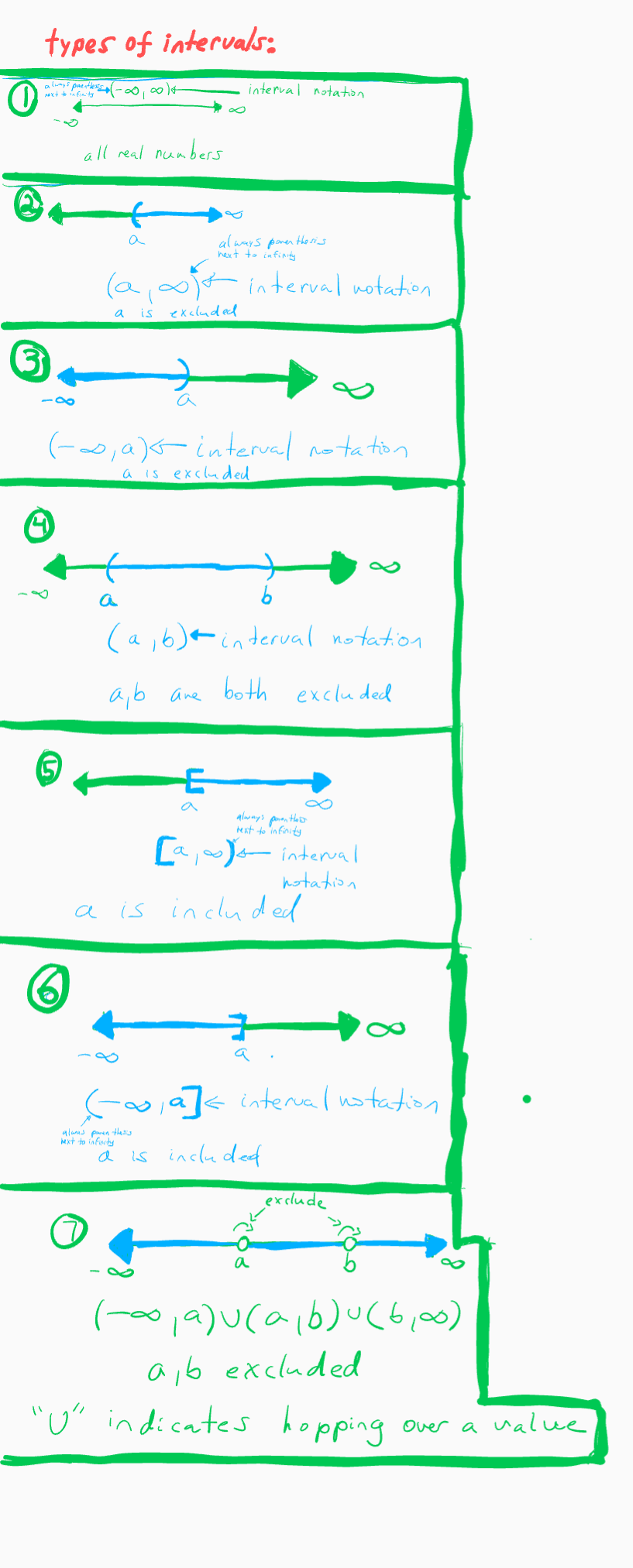
Interval notation is a way to describe a continuous range of values. The notation (a, b) represents all the numbers between a and b, but not including a and b themselves.

This can also be expressed using inequalities as a < x < b. Here's how the symbols correspond:

• (a, b): The parentheses mean that the values a and b are not included in the interval.
• a < x < b: The less-than symbols mean that x must be greater than a and less than b.
• (: The left parenthesis corresponds to the “greater than” symbol < for the lower bound a, meaning x must be greater than a.
• ): The right parenthesis corresponds to the “less than” symbol < for the upper bound b, meaning x must be less than b.

Examples:

(3, 7) is the same as 3 < x < 7, representing all numbers greater than 3 and less than 7.

(-2, 5) is the same as -2 < x < 5, representing all numbers greater than -2 and less than 5.

Summary: Interval notation (a, b) and inequality notation a < x < b are two ways to express the same continuous range of values. The parentheses in the interval notation correspond to the less-than symbols in the inequality notation, excluding the endpoints a and b.

Interval notation is a way to describe a continuous range of values. The notation [a, b) represents all the numbers between a and b, including a but not including b.

This can also be expressed using inequalities as a ≤ x < b. Here's how the symbols correspond:

• [a, b): The square bracket means that the value a is included in the interval, and the right parenthesis means that b is not included.
• a ≤ x < b: The "less than or equal to" symbol ≤ means that x can be equal to a or greater, and the "less than" symbol < means that x must be less than b.
• [: The left square bracket corresponds to the “less than or equal to” symbol ≤ for the lower bound a, meaning x can be equal to a or greater.
• ): The right parenthesis corresponds to the “less than” symbol < for the upper bound b, meaning x must be less than b.

Examples:

[3, 7) is the same as 3 ≤ x < 7, representing all numbers greater than or equal to 3 and less than 7.

[-2, 5) is the same as -2 ≤ x < 5, representing all numbers greater than or equal to -2 and less than 5.

Summary: Interval notation [a, b) and inequality notation a ≤ x < b are two ways to express the same continuous range of values, including the endpoint a but excluding b.

The inequality notation a < b ≤ c represents a range of values for b that are greater than a and less than or equal to c.

This inequality can be expressed using a combination of interval notations:

• (a, ∞): The left parenthesis means that a is not included, and the value of b must be greater than a.
• (−∞, c]: The right square bracket means that c is included, and the value of b must be less than or equal to c.
• The intersection of these two intervals, (a, c], represents all values greater than a and less than or equal to c.

Examples:

If a = 3 and c = 7, then 3 < b ≤ 7 represents all numbers greater than 3 and less than or equal to 7, corresponding to the interval (3, 7].

If a = -2 and c = 5, then -2 < b ≤ 5 represents all numbers greater than -2 and less than or equal to 5, corresponding to the interval (-2, 5].

Summary: The inequality notation a < b ≤ c can be expressed using the interval notation (a, c], representing a continuous range of values for b, where b is greater than a and less than or equal to c.

The inequality notation a ≤ x ≤ b represents a range of values for x that are greater than or equal to a and less than or equal to b.

This can be expressed using interval notation as [a, b]. Here’s how the symbols correspond:

• a ≤ x ≤ b: The “less than or equal to” symbols ≤ mean that x can be equal to a or greater, and equal to b or less.
• [a, b]: The square brackets mean that the values a and b are included in the interval.
• [: The left square bracket corresponds to the “less than or equal to” symbol ≤ for the lower bound a, meaning x can be equal to a or greater.
• ]: The right square bracket corresponds to the “less than or equal to” symbol ≤ for the upper bound b, meaning x can be equal to b or less.

Examples:

If a = 3 and b = 7, then a ≤ x ≤ b is the same as 3 ≤ x ≤ 7, representing all numbers greater than or equal to 3 and less than or equal to 7, corresponding to the interval [3, 7].

If a = -2 and b = 5, then a ≤ x ≤ b is the same as -2 ≤ x ≤ 5, representing all numbers greater than or equal to -2 and less than or equal to 5, corresponding to the interval [-2, 5].

Summary: The inequality notation a ≤ x ≤ b and the interval notation [a, b] are two ways to express the same continuous range of values, including the endpoints a and b.