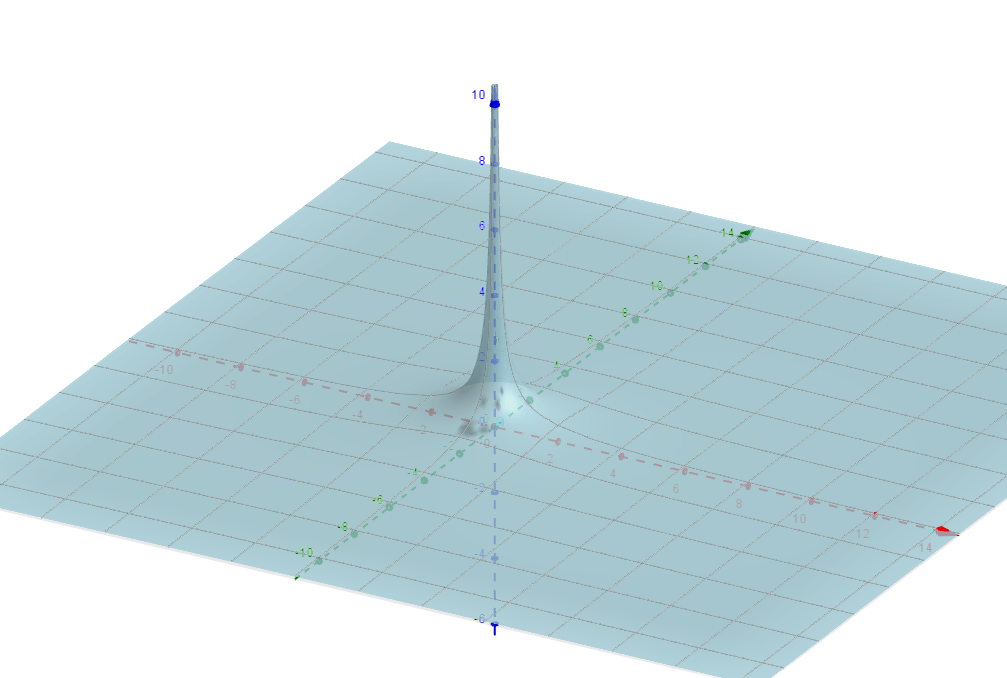
The 3D plot of the modulus of 1/z, where z is a complex number (x + yi), highlights a significant feature of complex analysis. As z approaches the origin of the complex plane (0 + 0i), the modulus (which represents the distance from the origin) grows infinitely large. This is visualized as a spike or a peak at the origin, where the height represents the magnitude of the modulus. The surface around the peak slopes downward as we move away from the origin, indicating that the modulus decreases with distance from the origin. The symmetry of the plot reflects the fact that the modulus of a complex number is the same regardless of the direction from which the origin is approached.