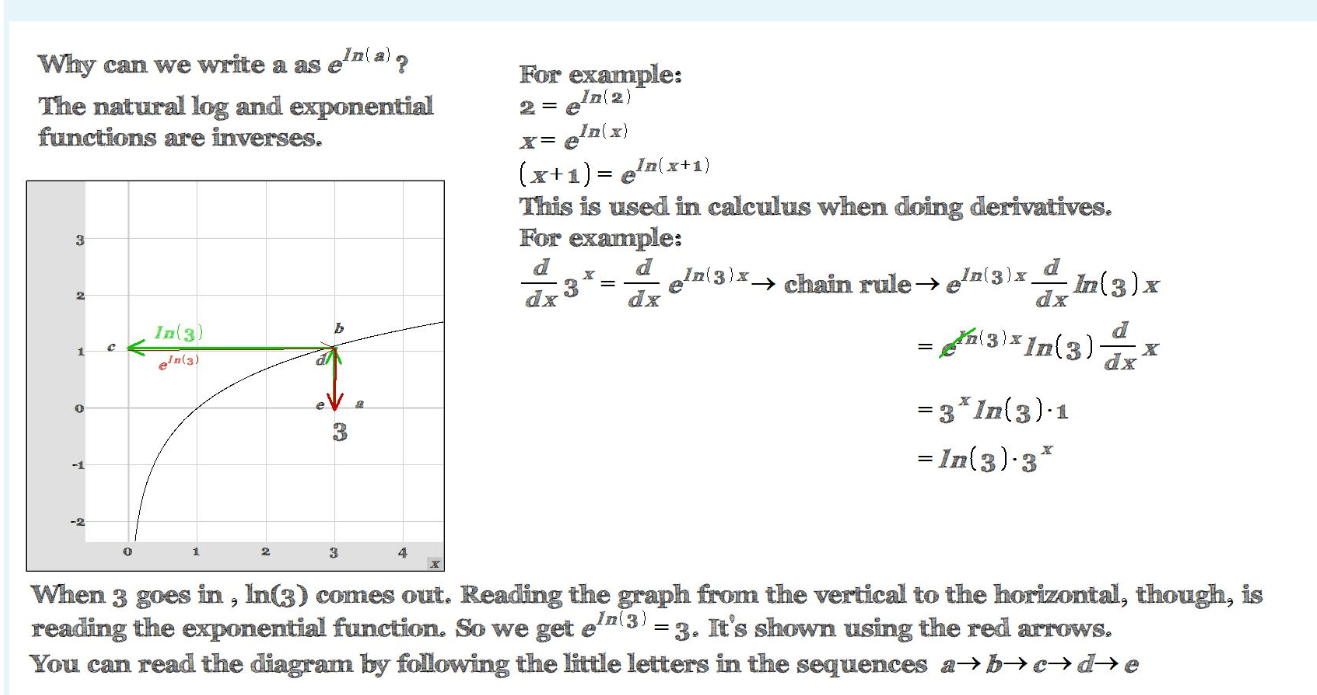
The image you sent me shows the relationship between the natural logarithm and exponential functions. The natural logarithm function is denoted by ln(x) and the exponential function is denoted by e^x. The two functions are inverses of each other, which means that for any input x, ln(e^x) = x and e^ln(x) = x.
The image shows this relationship by plotting the graphs of the two functions. The natural logarithm function is the inverse of the exponential function, so the graphs of the two functions are reflections of each other across the line y=x.
The image also shows how the natural logarithm function can be used to solve exponential equations. For example, the equation e^x = 3 can be solved by taking the natural logarithm of both sides of the equation. This gives us ln(e^x) = ln(3), which simplifies to x = ln(3).
The natural logarithm function is a useful tool for solving exponential equations and for understanding the relationship between exponential and logarithmic functions. It is also used in many other areas of mathematics, such as calculus and statistics.
Here are some additional details about the image:
The red arrows show how the input to the natural logarithm function is related to the output of the exponential function. For example, the input 3 to the natural logarithm function gives an output of ln(3), which is the value that must be raised to the power of e to get 3.
The blue arrows show how the derivative of the exponential function can be found using the natural logarithm function. The derivative of e^x is e^x, but this can be written as ln(e^x) = x using the natural logarithm function.