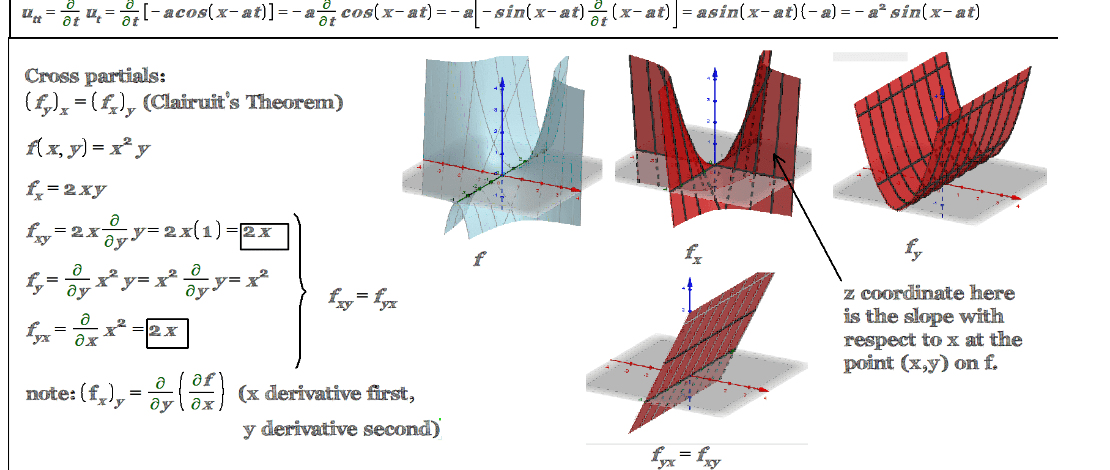
Understanding Second Partial Derivatives with a Quadratic Function
Let’s consider a function of two variables, x and y. The function is f(x, y) = x²y + xy². This function is a combination of quadratic and linear terms.
To find the second partial derivatives, we first compute the first partial derivatives. The first partial derivative with respect to x, denoted as ∂f/∂x, is found by differentiating f(x, y) with respect to x while treating y as a constant. This gives us ∂f/∂x = 2xy + y².
Similarly, the first partial derivative with respect to y, denoted as ∂f/∂y, is found by differentiating f(x, y) with respect to y while treating x as a constant. This gives us ∂f/∂y = x² + 2xy.
Next, we compute the second partial derivatives. The second partial derivative with respect to x, denoted as ∂²f/∂x², is found by differentiating ∂f/∂x with respect to x while treating y as a constant. This gives us ∂²f/∂x² = 2y.
The second partial derivative with respect to y, denoted as ∂²f/∂y², is found by differentiating ∂f/∂y with respect to y while treating x as a constant. This gives us ∂²f/∂y² = 2x.
The mixed second partial derivatives, denoted as ∂²f/∂x∂y and ∂²f/∂y∂x, are found by differentiating ∂f/∂x with respect to y and ∂f/∂y with respect to x, respectively. In this case, they are equal, and we get ∂²f/∂x∂y = ∂²f/∂y∂x = 2x + 2y.
The second partial derivatives give us information about the curvature of the function in different directions. In this case, ∂²f/∂x² and ∂²f/∂y² tell us about the curvature in the x and y directions, respectively, while ∂²f/∂x∂y = ∂²f/∂y∂x tell us about the curvature in the direction diagonal to the x and y axes.

Exploring Second Partial Derivatives with an Exponential Function
Let’s consider a function of two variables, x and y. The function is \(f(x, y) = e^{xy}\). This function is an exponential function where the exponent is a product of x and y.
To find the second partial derivatives, we first compute the first partial derivatives. The first partial derivative with respect to x, denoted as \(\frac{\partial f}{\partial x}\), is found by differentiating \(f(x, y)\) with respect to x while treating y as a constant. This gives us \(\frac{\partial f}{\partial x} = ye^{xy}\).
Similarly, the first partial derivative with respect to y, denoted as \(\frac{\partial f}{\partial y}\), is found by differentiating \(f(x, y)\) with respect to y while treating x as a constant. This gives us \(\frac{\partial f}{\partial y} = xe^{xy}\).
Next, we compute the second partial derivatives. The second partial derivative with respect to x, denoted as \(\frac{\partial^2 f}{\partial x^2}\), is found by differentiating \(\frac{\partial f}{\partial x}\) with respect to x while treating y as a constant. This gives us \(\frac{\partial^2 f}{\partial x^2} = y^2e^{xy}\).
The second partial derivative with respect to y, denoted as \(\frac{\partial^2 f}{\partial y^2}\), is found by differentiating \(\frac{\partial f}{\partial y}\) with respect to y while treating x as a constant. This gives us \(\frac{\partial^2 f}{\partial y^2} = x^2e^{xy}\).
The mixed second partial derivatives, denoted as \(\frac{\partial^2 f}{\partial x\partial y}\) and \(\frac{\partial^2 f}{\partial y\partial x}\), are found by differentiating \(\frac{\partial f}{\partial x}\) with respect to y and \(\frac{\partial f}{\partial y}\) with respect to x, respectively. In this case, they are equal, and we get \(\frac{\partial^2 f}{\partial x\partial y} = \frac{\partial^2 f}{\partial y\partial x} = (1 + xy)e^{xy}\).
The second partial derivatives give us information about the curvature of the function in different directions. In this case, \(\frac{\partial^2 f}{\partial x^2}\) and \(\frac{\partial^2 f}{\partial y^2}\) tell us about the curvature in the x and y directions, respectively, while \(\frac{\partial^2 f}{\partial x\partial y} = \frac{\partial^2 f}{\partial y\partial x}\) tell us about the curvature in the direction diagonal to the x and y axes.
The second partial derivatives give us information about the curvature of the function in different directions. If you imagine walking on the landscape of this function, ∂²f/∂x² and ∂²f/∂y² tell you about the steepness of the hills or valleys you encounter as you walk in the x and y directions, respectively. Larger values mean steeper slopes, while smaller values mean gentler slopes.
The mixed second partial derivatives, ∂²f/∂x∂y and ∂²f/∂y∂x, tell you about the steepness of the landscape as you move diagonally, that is, in both x and y directions simultaneously. If these values are positive, the landscape increases fastest when moving along the positive diagonal direction (increasing both x and y). If they are negative, the landscape increases fastest when moving along the negative diagonal direction (increasing one of x or y while decreasing the other).
In our specific case, ∂²f/∂x∂y = ∂²f/∂y∂x = (1 + xy)e^(xy) is always positive for positive x and y, indicating the landscape increases fastest along the positive diagonal direction. The exact rate of increase depends on the values of x and y due to the xy term in the expression. This means that if you are walking on this landscape, you would experience the steepest climb when moving in a direction that is a mix of both x and y.