Tangent Plane Approximation Explained
The image you sent me shows an explanation of tangent plane approximation. Tangent plane approximation is a way to approximate the value of a function of two variables at a given point by a linear function.
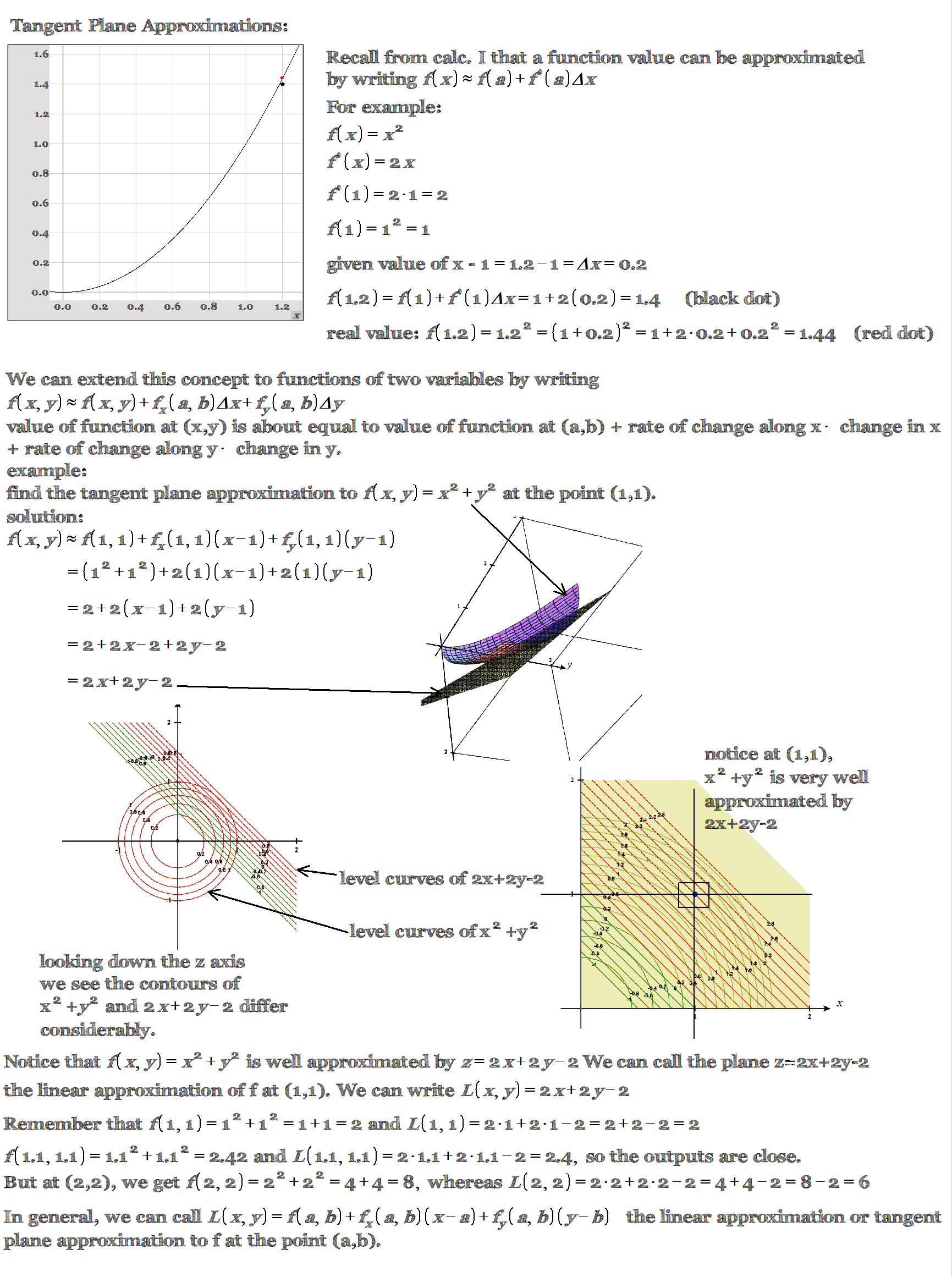
Approximation in One Variable:
The image starts by explaining how a function of one variable can be approximated by a linear function. The idea is to find the slope of the function at the given point, and then use that slope to find the equation of a line that passes through the point and has the same slope.
Extension to Two Variables:
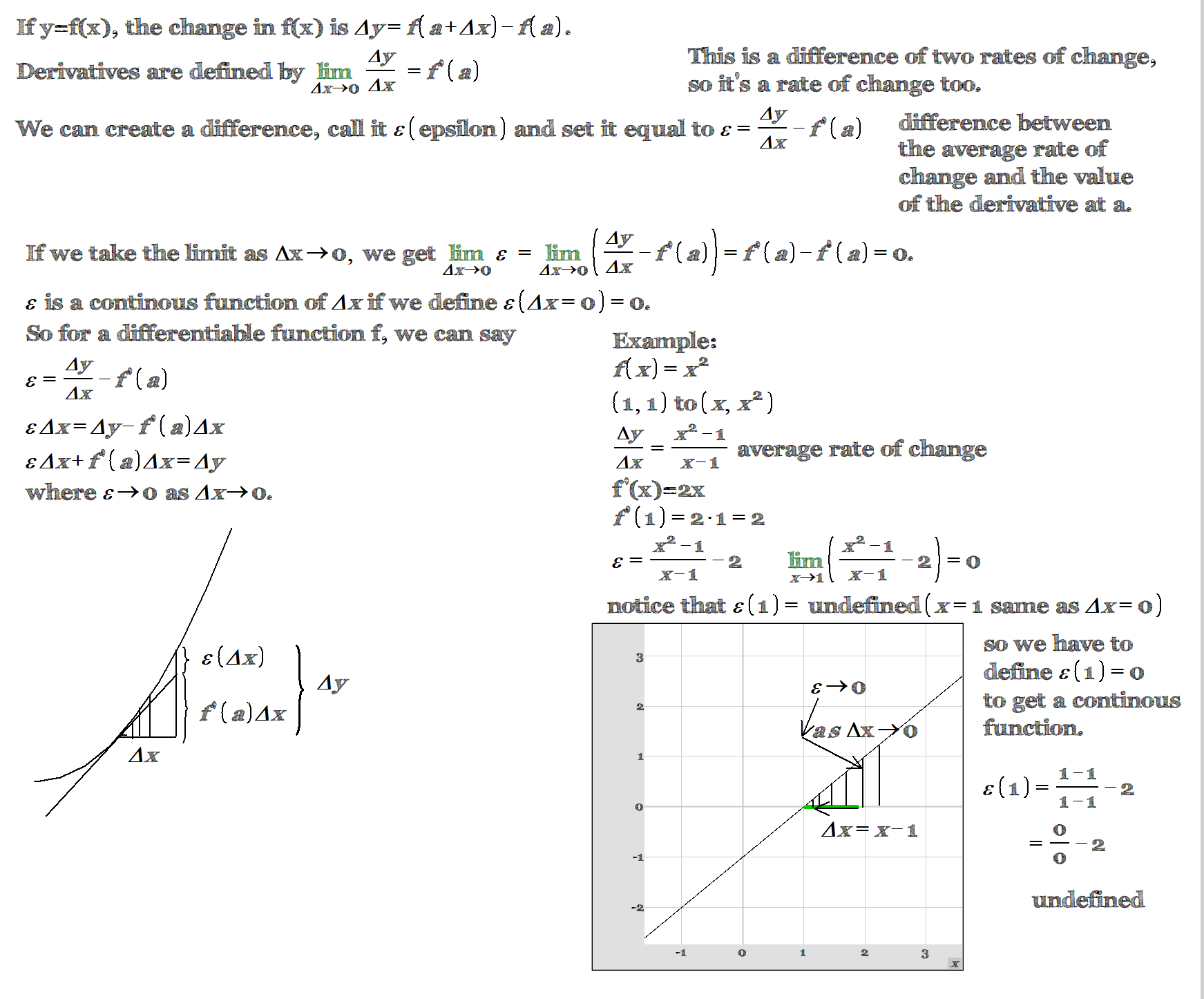
The image then goes on to explain how this concept can be extended to functions of two variables. In this case, the slope of the function is found by taking the partial derivatives of the function with respect to each variable. The partial derivative with respect to one variable tells us how much the function changes as that variable changes, while holding the other variable constant.
Tangent Plane Equation:
Once the partial derivatives have been found, the equation of the tangent plane can be written as follows:
L(x, y) = f(a, b) + fₓ(a, b)(x – a) + fᵧ(a, b)(y – b)
where (a, b) is the point of approximation, f(a, b) is the value of the function at that point, fₓ(a, b) is the partial derivative of the function with respect to x at that point, and fᵧ(a, b) is the partial derivative of the function with respect to y at that point.
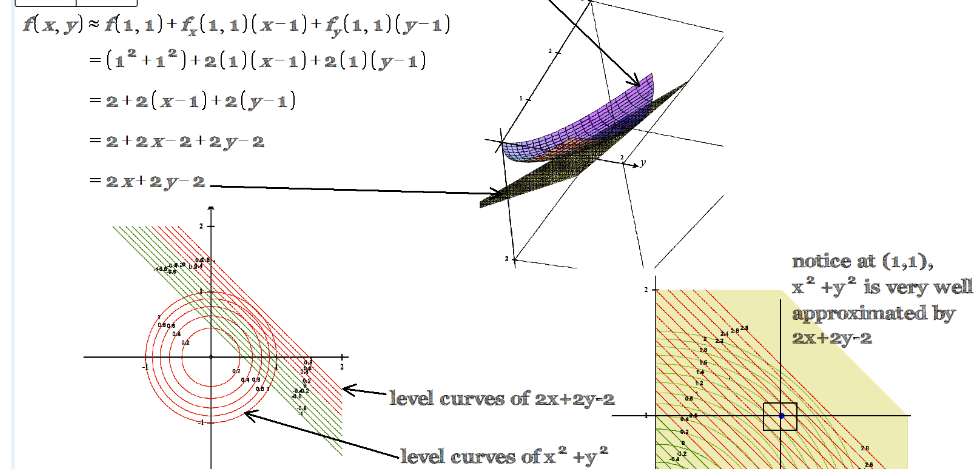
Example:
The image then shows an example of tangent plane approximation. The function f(x, y) = x + y is approximated at the point (1, 1) by the linear function z = 2x + 2y – 2. The image shows that the tangent plane approximation is a good approximation of the function near the point (1, 1).
I hope this analysis of the image is helpful. Let me know if you have any other questions.