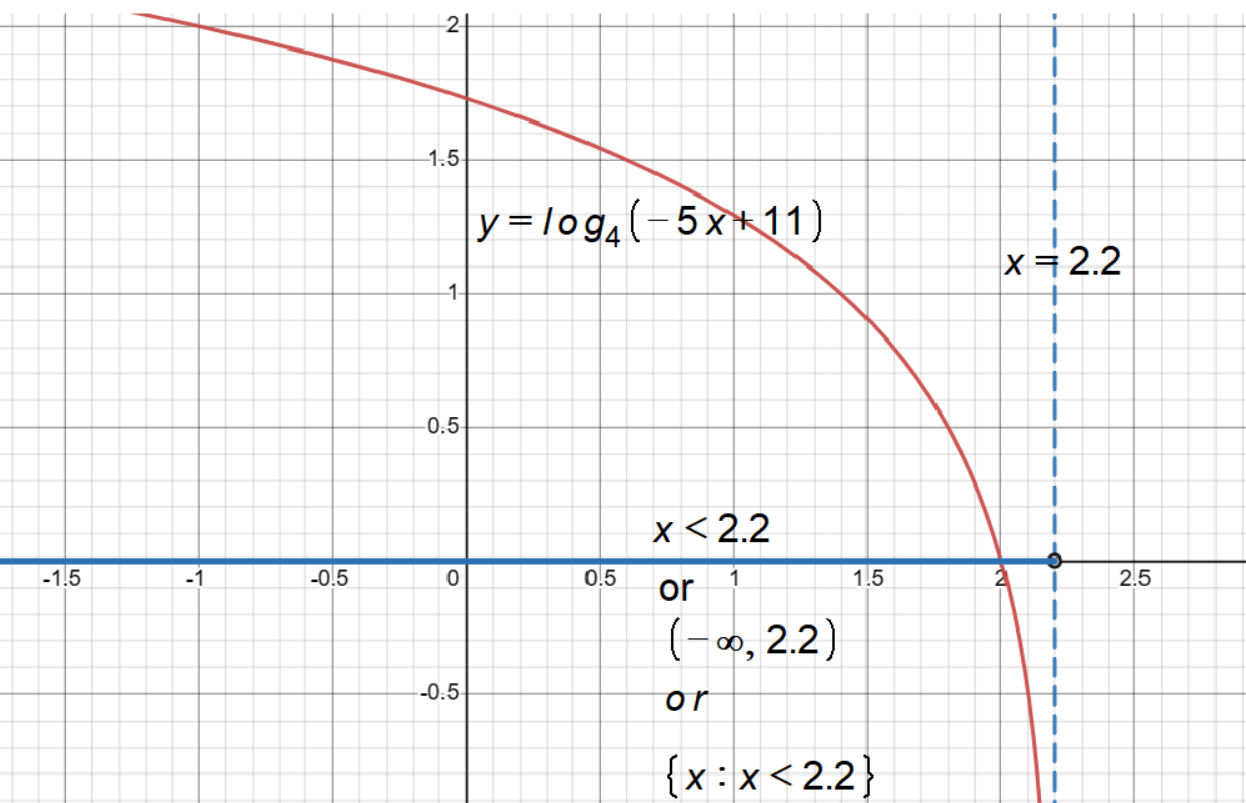Finding the Domain of log₄(-5x + 11): A Symbol-by-Symbol Guide

Step 1: Understand the Function and Symbols

We are looking at the function log₄(-5x + 11). Here, ‘log’ stands for logarithm, ‘₄’ is the base of the logarithm, and ‘(-5x + 11)’ is the argument of the logarithm.

Step 2: Set Up the Inequality

For a logarithm to be defined, the argument inside must be greater than zero. We set up the inequality:

-5x + 11 > 0

Here, ‘>’ means ‘greater than’, ‘0’ is zero, ‘-5x’ represents negative five times x, and ’11’ is eleven.

Step 3: Solve the Inequality

We want to isolate x on one side. First, we move -5x to the other side by adding 5x to both sides:

11 > 5x

Next, we divide both sides by -5. Remember, dividing by a negative number reverses the inequality:

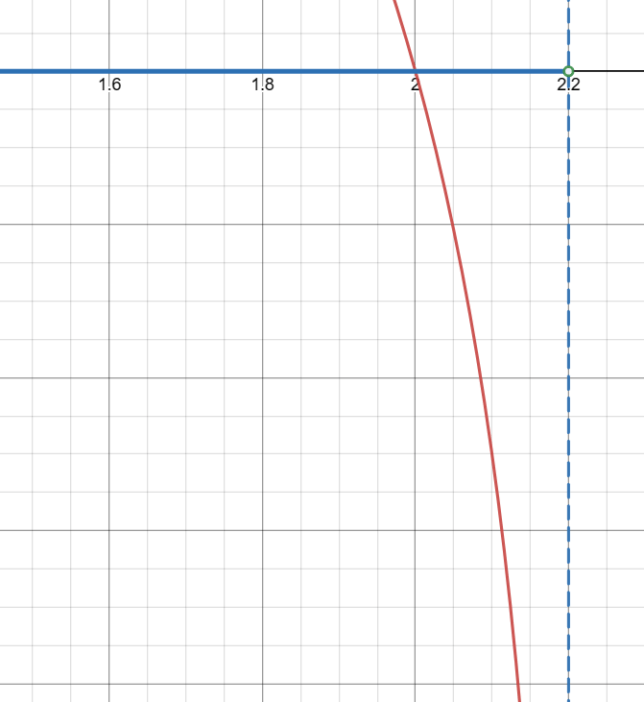
x < 2.2

Here, ‘<' means 'less than', and '2.2' is two point two.

Step 4: Write the Domain

The domain of log₄(-5x + 11) is all x-values that are less than 2.2.

Conclusion

The function log₄(-5x + 11) is defined for x < 2.2. This means you can plug any x-value less than 2.2 into the function and it will be valid.

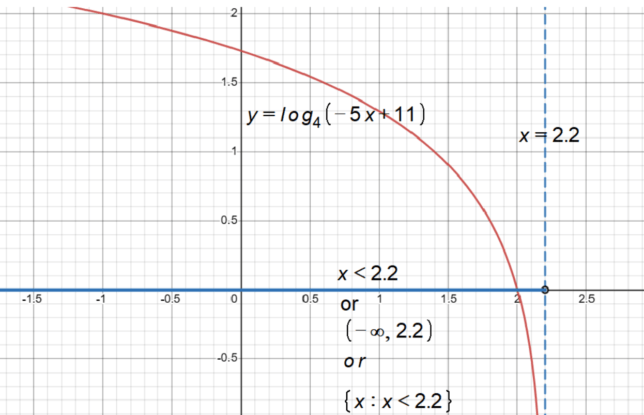
Decoding the Domain of log₄(-5x + 11) in Interval Notation

Step 1: The Inequality x < 2.2

We found that the domain of log₄(-5x + 11) is x < 2.2. The symbol '<' means 'less than,' which tells us that x can be any number that is smaller than 2.2.

Step 2: The Opening Parenthesis (

In interval notation, the opening parenthesis ‘(‘ is used when the starting point is not included in the interval. Here, it signifies that numbers smaller than any real number are part of the domain, but not the ‘smallest’ number itself, which is represented by negative infinity.

Step 3: Negative Infinity

The symbol for negative infinity is a dash followed by the infinity symbol. It means that x can be as small as you can imagine, going all the way to negative infinity.

Step 4: The Comma

The comma separates the lower and upper bounds of the interval. It’s like saying “from this point to this point.”

Step 5: The Number 2.2

The number 2.2 is directly taken from the inequality x < 2.2. It serves as the upper bound of the interval, indicating that x can go up to, but not include, 2.2.

Step 6: The Closing Parenthesis )

The closing parenthesis ‘)’ is used when the endpoint is not included in the interval. This aligns with the inequality x < 2.2, where 2.2 is not included.

Step 7: Connecting the Inequality and Interval Notation

The inequality x < 2.2 tells us that x can be any number smaller than 2.2 but not 2.2 itself. This is precisely what the interval notation (-∞, 2.2) represents. The opening parenthesis and closing parenthesis make it clear that the endpoints are not included, just like in the inequality.

Conclusion

The interval notation (-∞, 2.2) is a compact way to express the same information as the inequality x < 2.2. It tells us that x can be any number greater than negative infinity and smaller than 2.2, without including the endpoints.

Decoding the Domain of log₄(-5x + 11) in Set-Builder Notation: A Symbol-by-Symbol Guide

Step 1: The Opening Brace {

The opening brace ‘{‘ indicates the start of the set. It tells us that we are about to define a set of numbers that belong to the domain.

Step 2: The Variable x

The variable ‘x’ represents the numbers that are in the domain. It’s what we’re solving for.

Step 3: The Vertical Bar |

The vertical bar ‘|’ is read as “such that” and separates the variable from the conditions that the variable must satisfy to be in the set.

Step 4: The Inequality x < 2.2

The inequality ‘x < 2.2' is the condition that x must satisfy to be in the domain. It comes directly from our earlier work, where we found that the domain of log₄(-5x + 11) is x < 2.2.

Step 5: The Closing Brace }

The closing brace ‘}’ indicates the end of the set. It tells us that we have finished defining the set of numbers that belong to the domain.

Step 6: Putting It All Together

When we put all these symbols together, we get {x | x < 2.2}. This is read as "the set of all x such that x is less than 2.2."

Conclusion

The set-builder notation {x | x < 2.2} is another way to represent the domain of log₄(-5x + 11). It includes all x-values that are less than 2.2, which is the same information conveyed by the inequality x < 2.2.