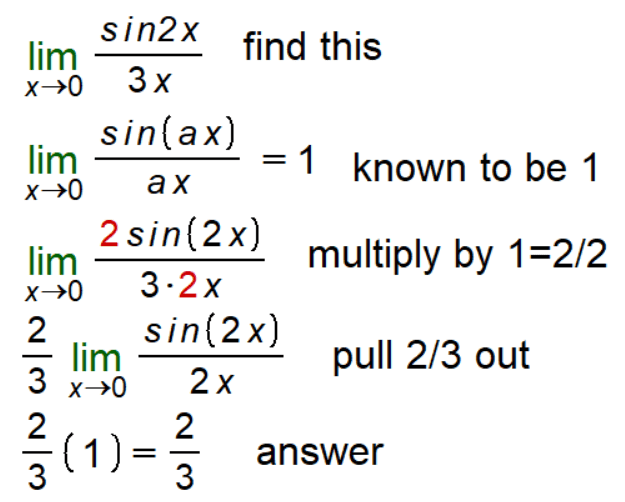Limit Expression Evaluation

This analysis focuses on evaluating the limit of a specific mathematical expression, namely \( \lim_{{x \rightarrow 0 }}\frac{{\sin(2x)}}{{3x}} \). In calculus, evaluating limits at a point is a fundamental concept. The process of evaluating this limit is broken down into several steps outlined below:

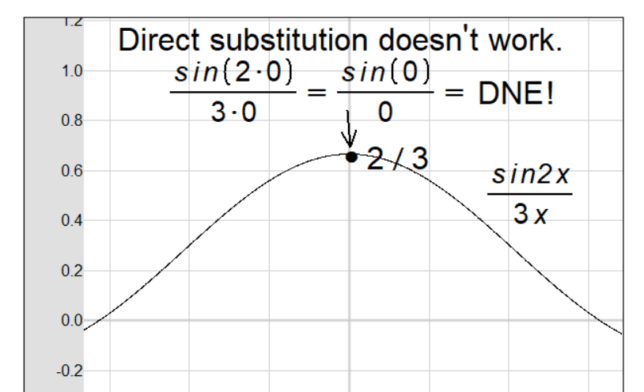
Initial Expression: The expression we are focusing on is \( \lim_{{x \rightarrow 0 }}\frac{{\sin(2x)}}{{3x}} \). This expression is a fraction where the numerator is the sine of \(2x\) and the denominator is \(3x\).

Known Limit: There’s a known limit in calculus, \( \lim_{{x \rightarrow 0 }}\frac{{\sin(ax)}}{{ax}} = 1 \), which is often referred to as the Sine Limit Lemma. This lemma is crucial for solving our original expression.

Expression Rewritten: By multiplying and dividing the expression by 2, we rewrite the expression as \( \lim_{{x \rightarrow 0 }}\frac{{2\sin(2x)}}{{3 \cdot 2x}} \). This step is taken to align our expression with the known limit.

Factor Out \( \frac{2}{3} \): We then factor out \( \frac{2}{3} \) from the expression, which gives us \( \frac{2}{3} \lim_{{x \rightarrow 0 }}\frac{{\sin(2x)}}{{2x}} \). This step simplifies the expression further.

Apply Known Limit: Now we apply the known limit to the expression inside the limit, resulting in \( \frac{2}{3} \cdot \left(1\right) = \frac{2}{3} \).

Result: After applying the known limit, we find that the final result of the original limit expression is \( \frac{2}{3} \). This demonstrates the process of breaking down and evaluating limit expressions using known results from calculus.