Unlock the Secrets: Finding the Domain and Range of f(x) = √(x² – 1)
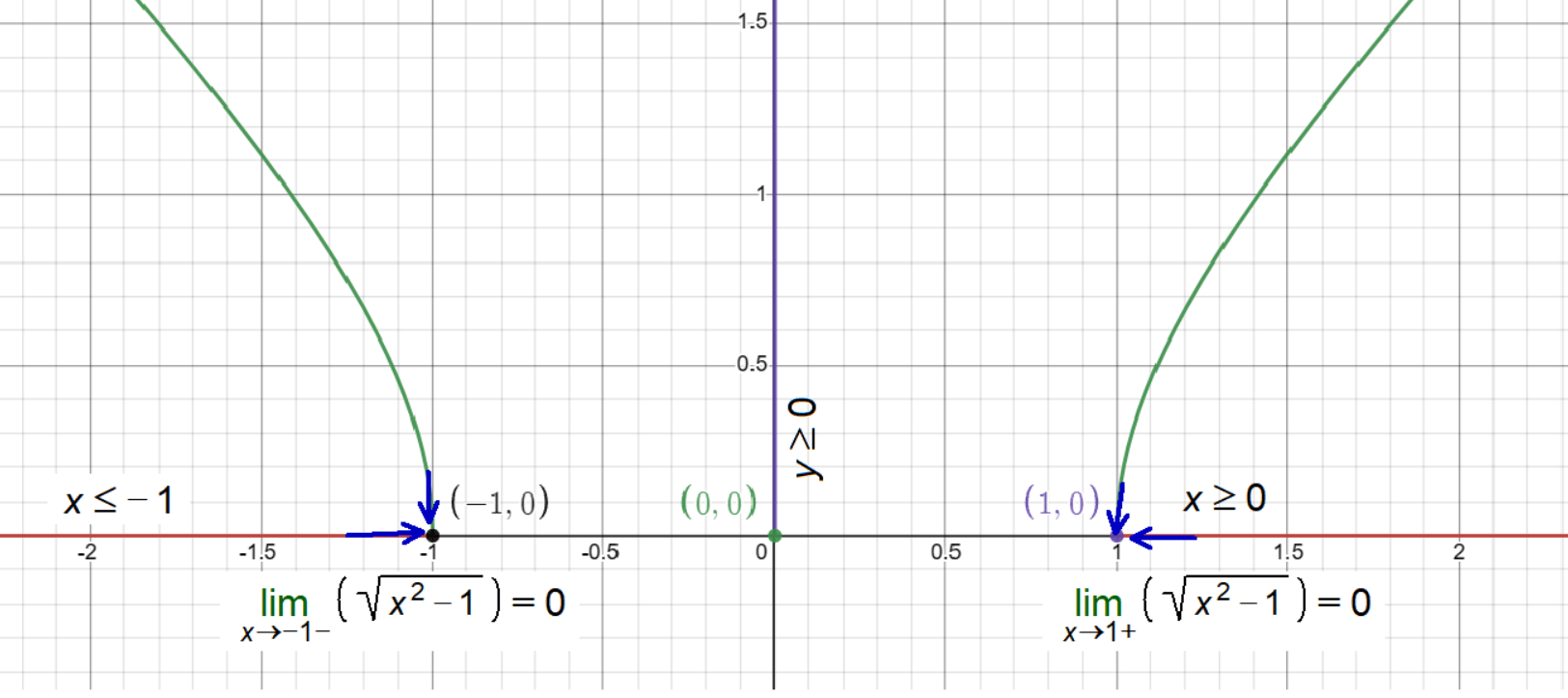
Finding the Domain
- Step 1: Identify the Radicand – The expression inside the square root is x² – 1.
- Step 2: Set Constraints – x² – 1 ≥ 0.
- Step 3: Solve for x – x ≤ -1 or x ≥ 1.
- Step 4: State the Domain – x ≤ -1 or x ≥ 1.
Finding the Range
- Step 1: Behavior of the Function – Outputs only non-negative values.
- Step 2: Minimum and Maximum of Radicand – Smallest value is 0, no upper limit.
- Step 3: State the Range – f(x) ≥ 0.
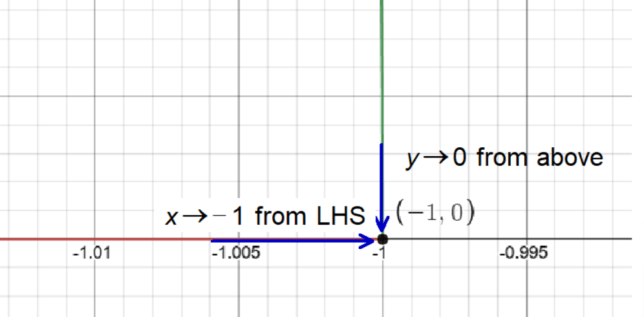
Decoding Limits: Unveiling the Limit of f(x) = √(x² – 1) as x Approaches -1 from the Left
Step 1: Identify the Function and Point of Interest
The function we’re examining is f(x) = √(x² – 1), and the point of interest is x = -1.
Step 2: Observe the Function’s Behavior
As x nears -1 from the left, the expression x² – 1 approaches zero.
Step 3: Evaluate the Limit
The square root of zero is zero, and so as x approaches -1 from the left, the function value also converges to zero.
Step 4: State the Limit
Thus, the limit of f(x) = √(x² – 1) as x approaches -1 from the left-hand side is zero.
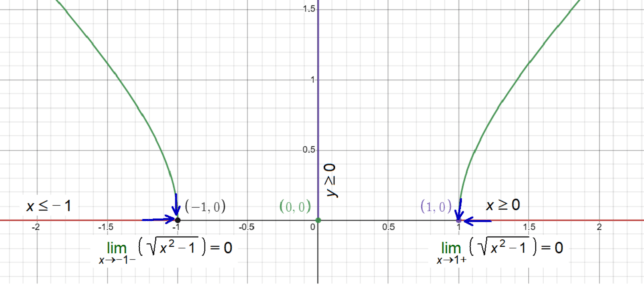
Decoding Limits: Unveiling the Limit of f(x) = √(x² – 1) as x Approaches 1 from the Right
Step 1: Identify the Function and Point of Interest
The function we’re examining is f(x) = √(x² – 1), and the point of interest is x = 1.
Step 2: Observe the Function’s Behavior
As x nears 1 from the right, the expression x² – 1 approaches zero.
Step 3: Evaluate the Limit
The square root of zero is zero, so as x approaches 1 from the right, the function value also converges to zero.
Step 4: State the Limit
Thus, the limit of f(x) = √(x² – 1) as x approaches 1 from the right-hand side is zero.