Convergence and Summation Bounds of Series
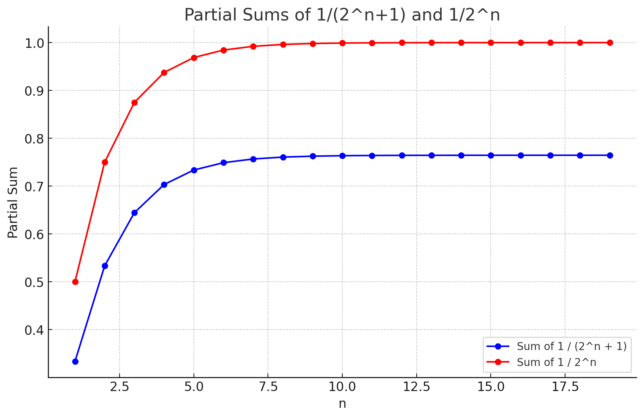
When examining the convergence of a series, it is often helpful to compare it to another series whose behavior is well understood. In this context, we consider the series with terms 1 / (2ⁿ + 1), which we are interested in, and compare it to the classic geometric series with terms 1 / 2ⁿ. The latter series is well-known to converge to a sum of 1 as n approaches infinity.
In our comparison, the red dots on the graph depict the terms of the geometric series 1 / 2ⁿ, and the sum of these terms from n=1 to infinity is exactly 1. This series serves as an upper bound for our series represented by the blue dots, 1 / (2ⁿ + 1). Since every term of our series is less than the corresponding term of the geometric series, it follows that the sum of our series must also be less than 1.
This comparison tells us that the sum of the series 1 / (2ⁿ + 1) is bounded above by 1. Therefore, not only do we know that our series converges, but we also have a clear upper limit on its sum. Such information is invaluable because it gives us a quantitative measure of the series’ behavior and ensures that the series does not diverge to infinity.
The concept of being ‘bounded above’ is a key idea in the study of series and sequences. For a series with positive terms, if it is bounded above and the terms are decreasing to zero, the series must converge. In this case, our original series is indeed bounded above by the geometric series and thus converges to a sum that is less than or equal to 1.
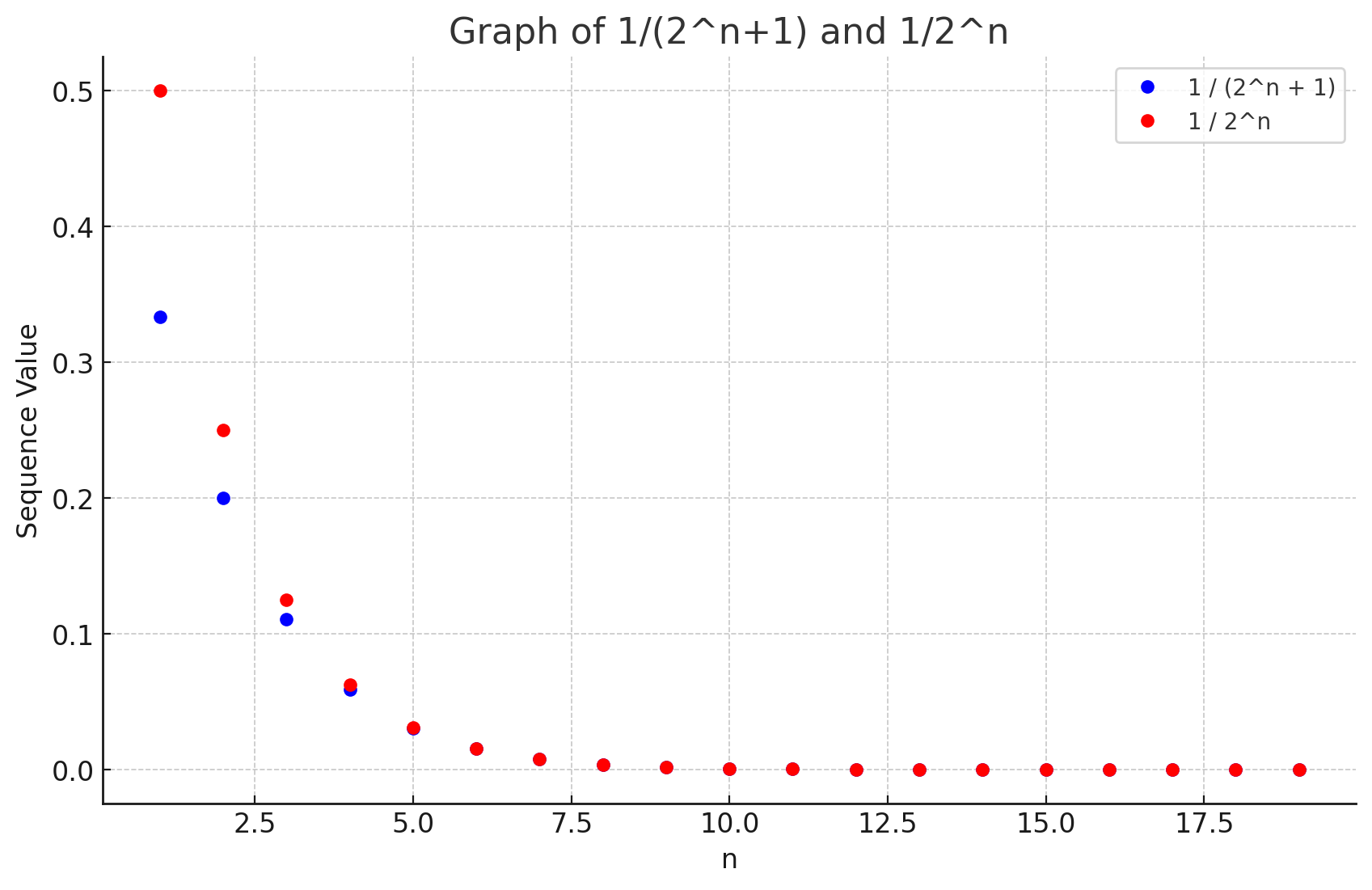
Here’s the graph of the two sequences, 1 / (2ⁿ + 1) and 1 / 2ⁿ, represented as blue and red dots, respectively. As you can see, the red dots (1 / 2ⁿ) are always above the blue dots (1 / (2ⁿ + 1)), demonstrating that the terms of 1 / (2ⁿ + 1) are indeed smaller than those of 1 / 2ⁿ for all n in the range we’ve plotted. This visual supports the argument that if 1 / 2ⁿ converges, so does 1 / (2ⁿ + 1), by the Comparison Test.