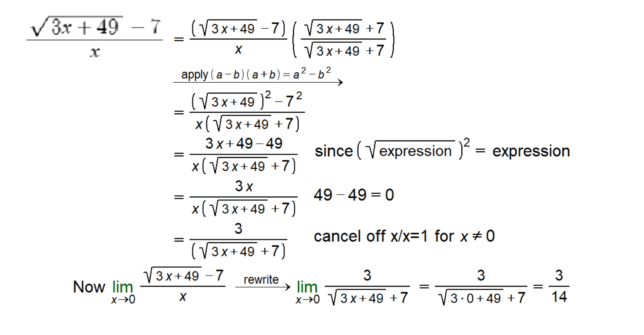Unveiling Every Single Step: Limit of \( \frac{\sqrt{3x + 49} – 7}{x} \) as \( x \) Approaches 0
Step 1: The Direct Substitution Attempt
Starting with the original function:
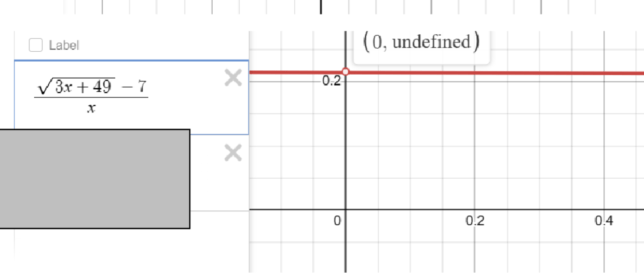
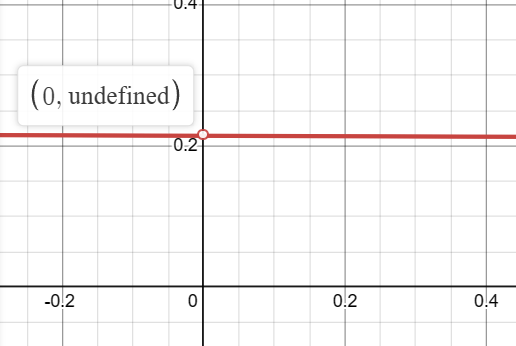
\[ \lim_{{x \to 0}} \frac{\sqrt{3x + 49} – 7}{x} \]
Direct substitution gives:
\[ \frac{\sqrt{3 \cdot 0 + 49} – 7}{0} = \frac{\sqrt{49} – 7}{0} = \frac{0}{0} \]
This is indeterminate, so we’ll need another method.
Step 2: Rationalizing the Numerator
To eliminate the square root in the numerator, we’ll multiply by the conjugate:
\[ \frac{\sqrt{3x + 49} + 7}{\sqrt{3x + 49} + 7} \]
Performing the multiplication gives:
\[ \frac{\sqrt{3x + 49} \cdot \sqrt{3x + 49} + 7 \cdot \sqrt{3x + 49} – 7 \cdot \sqrt{3x + 49} – 7 \cdot 7}{x \cdot (\sqrt{3x + 49} + 7)} \]
Step 3: Simplifying
Combining terms, we get:
\[ \frac{3x + 49 – 49}{x(\sqrt{3x + 49} + 7)} = \frac{3x}{x(\sqrt{3x + 49} + 7)} \]
Now, the \(x\) terms can be canceled:
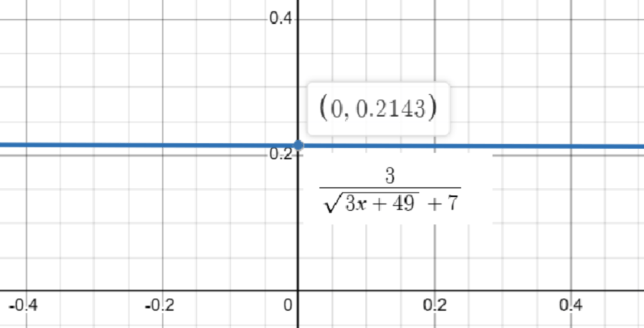
\[ \frac{3}{\sqrt{3x + 49} + 7} \]
Step 4: Final Direct Substitution
With the simplified form, let’s try plugging in \(x = 0\) again:
\[ \lim_{{x \to 0}} \frac{3}{\sqrt{3x + 49} + 7} = \frac{3}{\sqrt{0 + 49} + 7} = \frac{3}{\sqrt{49} + 7} = \frac{3}{7 + 7} = \frac{3}{14} \]
Step 5: The Limit is Revealed!
The limit of \( \frac{\sqrt{3x + 49} – 7}{x} \) as \( x \) approaches 0 is \( \frac{3}{14} \).
By meticulously breaking down each algebraic move, we’ve cracked the case. Math has never been so transparent!