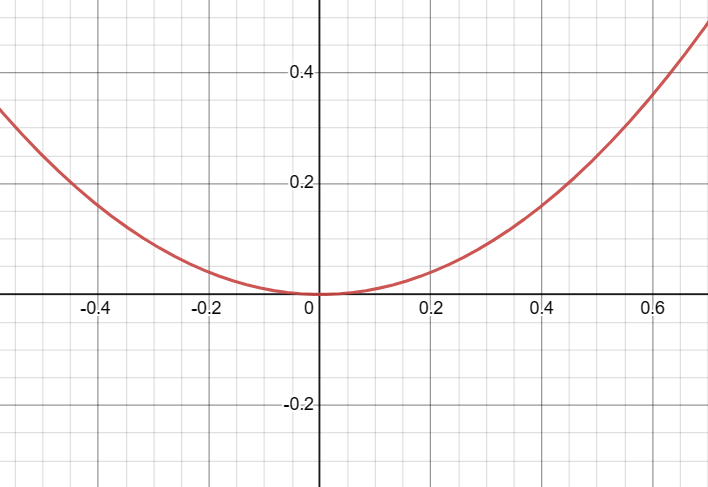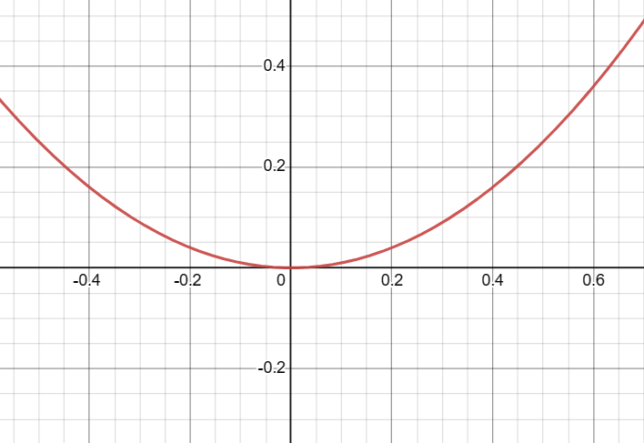
Behavior Close to x=0 for x²
The function f(x) = x² behaves quadratically around x = 0. As you approach 0 from either the left or the right, the function also approaches 0.
- As x approaches 0 from the left, f(x) approaches 0 from above.
- As x approaches 0 from the right, f(x) approaches 0 from above.
This behavior indicates that the root at x = 0 has a multiplicity of 2.
Because the root has a multiplicity of 2, the graph of the function “bounces” off the x-axis at x = 0.
Table of Calculations Close to x=0 for x²
| x Value | f(x) = x² |
|---|---|
| -0.1 | 0.01 |
| -0.01 | 0.0001 |
| -0.001 | 0.000001 |
| 0 | 0 |
| 0.001 | 0.000001 |
| 0.01 | 0.0001 |
| 0.1 | 0.01 |
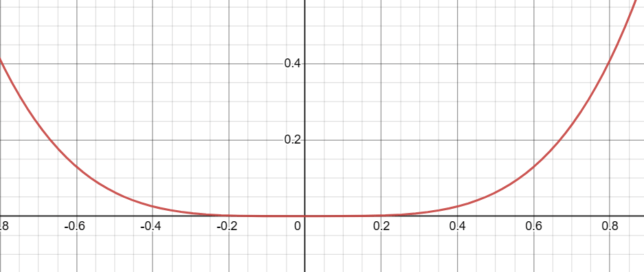
Behavior Close to x=0 for x⁴
The function f(x) = x⁴ behaves in a quartic manner around x = 0. As you approach 0 from either the left or the right, the function also approaches 0.
- As x approaches 0 from the left, f(x) approaches 0 from above.
- As x approaches 0 from the right, f(x) approaches 0 from above.
This behavior indicates that the root at x = 0 has a multiplicity of 4.
Because the root has a multiplicity of 4, the graph of the function “bounces” off the x-axis at x = 0, similar to x² but with a more pronounced flattening.
Table of Calculations Close to x=0 for x⁴
| x Value | f(x) = x⁴ |
|---|---|
| -0.1 | 0.0001 |
| -0.01 | 0.00000001 |
| -0.001 | 0.000000000001 |
| 0 | 0 |
| 0.001 | 0.000000000001 |
| 0.01 | 0.00000001 |
| 0.1 | 0.0001 |
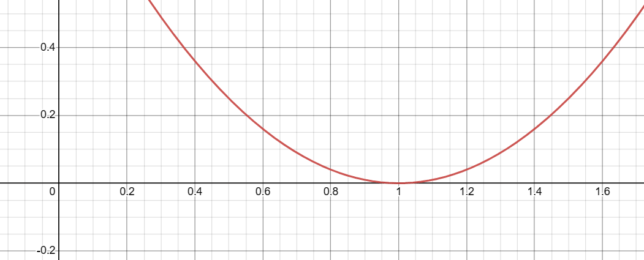
Behavior Close to x=1 for (x-1)²
The function f(x) = (x-1)² behaves quadratically around x = 1, similar to how f(x) = x² behaves around x = 0.
- As x approaches 1 from the left, f(x) approaches 0 from above.
- As x approaches 1 from the right, f(x) approaches 0 from above.
This behavior indicates that the root at x = 1 has a multiplicity of 2, just like the root at x = 0 for f(x) = x².
The graph of f(x) = (x-1)² is essentially the graph of f(x) = x² shifted one unit to the right. This shift does not affect the multiplicity of the root or the general shape of the graph near the root; it simply moves the location of the root from x = 0 to x = 1.
Table of Calculations Close to x=1 for (x-1)²
| x Value | f(x) = (x-1)² |
|---|---|
| 0.9 | 0.01 |
| 0.99 | 0.0001 |
| 0.999 | 0.000001 |
| 1 | 0 |
| 1.001 | 0.000001 |
| 1.01 | 0.0001 |
| 1.1 | 0.01 |
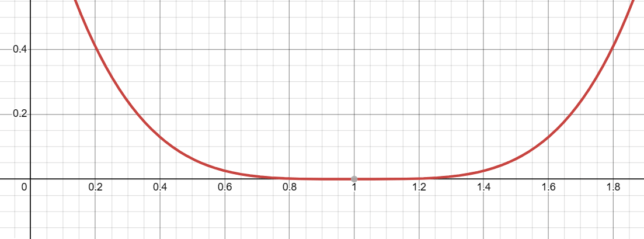
Behavior Close to x=1 for (x-1)⁴
The function f(x) = (x-1)⁴ behaves in a quartic manner around x = 1, similar to how f(x) = x⁴ behaves around x = 0.
- As x approaches 1 from the left, f(x) approaches 0 from above.
- As x approaches 1 from the right, f(x) approaches 0 from above.
This behavior indicates that the root at x = 1 has a multiplicity of 4, just like the root at x = 0 for f(x) = x⁴.
The graph of f(x) = (x-1)⁴ is essentially the graph of f(x) = x⁴ shifted one unit to the right. This shift does not affect the multiplicity of the root or the general shape of the graph near the root; it simply moves the location of the root from x = 0 to x = 1.
Table of Calculations Close to x=1 for (x-1)⁴
| x Value | f(x) = (x-1)⁴ |
|---|---|
| 0.9 | 0.0001 |
| 0.99 | 0.00000001 |
| 0.999 | 0.000000000001 |
| 1 | 0 |
| 1.001 | 0.000000000001 |
| 1.01 | 0.00000001 |
| 1.1 | 0.0001 |
Understanding the Nature of Roots in (x-a)ⁿ for Even n
When dealing with a function like f(x) = (x-a)ⁿ where n is an even integer, it’s important to understand what the exponent means in terms of roots.
Case of (x-a)²
For example, in the case of f(x) = (x-a)², this can be expanded as:
(x-a)² = (x-a)(x-a)
This shows that x = a is a root that appears twice, making it a “double root.”
General Case of (x-a)ⁿ
In the general case of f(x) = (x-a)ⁿ, the root x = a will appear n times. This is known as a root with “multiplicity” of n.
As x approaches a from both the left and the right, f(x) approaches 0 from above. This behavior indicates that the root at x = a has a multiplicity of n.
When you’re very close to the root, a higher n will make the function appear flatter near the root. The graph will approach the x-axis more gradually.
For different values of a such as -1, 0, 1.5, etc., the graph will simply shift horizontally but retain the same general shape and behavior around the root.