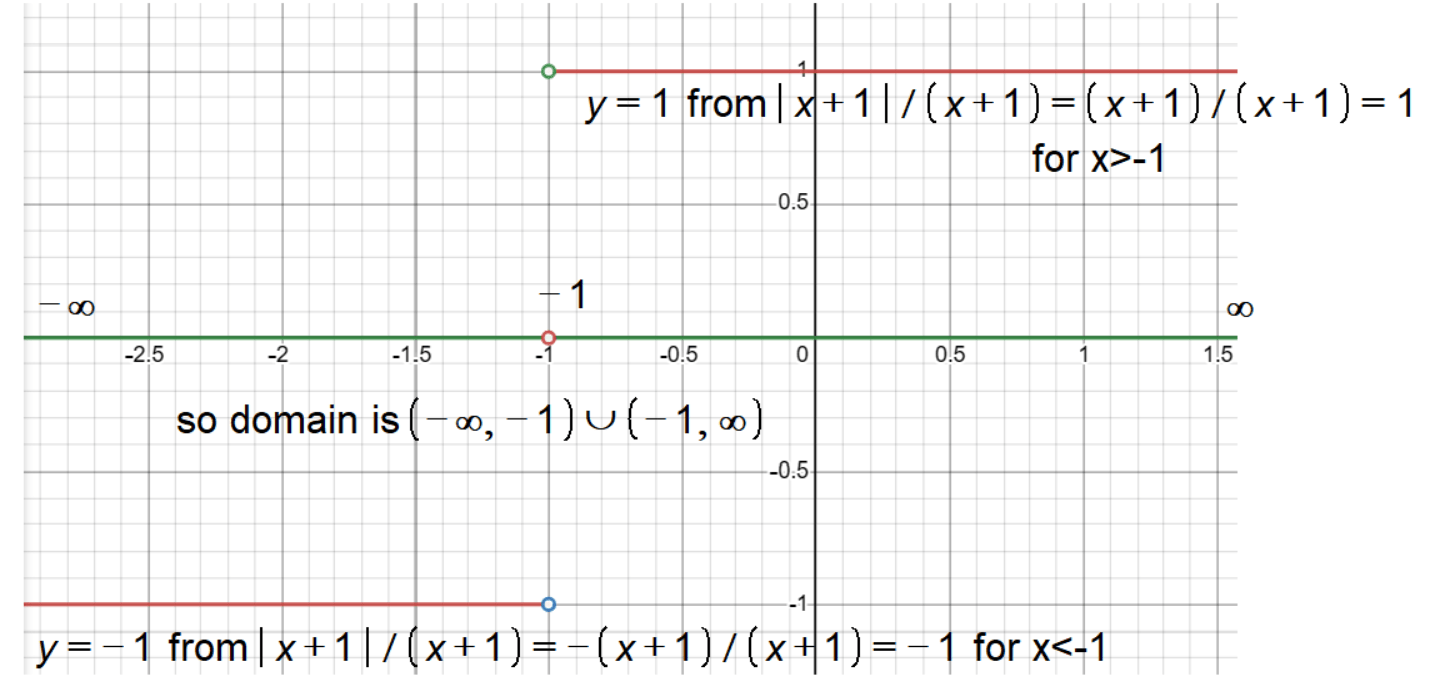Unveiling the Paradox: Why the Limit of |x+1|/(x+1) Appears
| x | Substituted Fraction (|x+1|/(x+1)) | Result of |x+1|/(x+1) |
|---|---|---|
| -0.9 | |-0.9+1|/(-0.9+1) | 1 |
| -0.99 | |-0.99+1|/(-0.99+1) | 1 |
| -0.999 | |-0.999+1|/(-0.999+1) | 1 |
| -0.9999 | |-0.9999+1|/(-0.9999+1) | 1 |
The table shows that as x gets closer to -1 from the right-hand side, the value of |x+1|/(x+1) approaches 1.
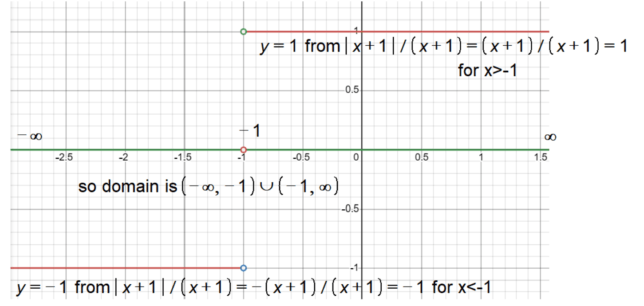
Unlocking the Enigma: The Limit of |x+1|/(x+1) as x Nears -1 from the LHS
| x | Substituted Fraction (|x+1|/(x+1)) | Result of |x+1|/(x+1) |
|---|---|---|
| -1.1 | |-1.1+1|/(-1.1+1) | -1 |
| -1.01 | |-1.01+1|/(-1.01+1) | -1 |
| -1.001 | |-1.001+1|/(-1.001+1) | -1 |
| -1.0001 | |-1.0001+1|/(-1.0001+1) | -1 |
The table shows that as x gets closer to -1 from the left-hand side, the value of |x+1|/(x+1) approaches -1.
Domain of the Function |x + 1|/(x + 1)
- Interval Notation: (-∞, -1) ∪ (-1, ∞)
- Set-Builder Notation: { x ∈ R : x ≠ -1 }
- In Words: All real numbers except x = -1