Derivative of |x| at \(x = 0\) using Definition
Let’s find the derivative of the absolute value function, \(|x|\), at \(x = 0\) using the definition of a derivative.
Definition of Derivative:
The derivative of a function \(f(x)\) at a point \(a\) is defined as:
\(f'(a) = \lim_{{h \to 0}} \frac{f(a + h) – f(a)}{h}\)
Calculating the Derivative at \(x = 0\):
For \(|x|\), we have:
\(f(x) = |x|\)
\(f(0) = |0| = 0\)
Now, let’s compute the derivative at \(x = 0\):
\(f'(0) = \lim_{{h \to 0}} \frac{|0 + h| – |0|}{h}\)
As \(h\) approaches 0, we have:
\(f'(0) = \lim_{{h \to 0}} \frac{h}{h}\)
\(f'(0) = \lim_{{h \to 0}} 1\)
\(f'(0) = 1\)
Result:
The derivative of \(|x|\) at \(x = 0\) is 1.
Derivative of |x| at \(x = 0\) from the Left-Hand Side (LHS) using Definition
Let’s find the derivative of the absolute value function, \(|x|\), at \(x = 0\) from the left-hand side (LHS) using the definition of a derivative.
Definition of Derivative:
The derivative of a function \(f(x)\) at a point \(a\) is defined as:
\(f'(a) = \lim_{{h \to 0}} \frac{f(a + h) – f(a)}{h}\)
Calculating the Derivative at \(x = 0\) from the LHS:
For \(|x|\), we have:
\(f(x) = |x|\)
\(f(0) = |0| = 0\)
Now, let’s compute the derivative at \(x = 0\) from the LHS:
\(f'(0) = \lim_{{h \to 0^-}} \frac{|0 + h| – |0|}{h}\)
As \(h\) approaches 0 from the left, we have:
\(f'(0) = \lim_{{h \to 0^-}} \frac{-h}{h}\)
\(f'(0) = \lim_{{h \to 0^-}} -1\)
\(f'(0) = -1\)
Result:
The derivative of \(|x|\) at \(x = 0\) from the left-hand side (LHS) is -1.
Summary of \(|x|\) Derivative at \(x = 0\)
The derivative of \(|x|\) at \(x = 0\) has two distinct values:
From the right-hand side (RHS): \(f'(0) = 1\)
From the left-hand side (LHS): \(f'(0) = -1\)
Because the derivative has different values when approached from different sides, \(f'(0)\) does not exist or is undefined at \(x = 0\).
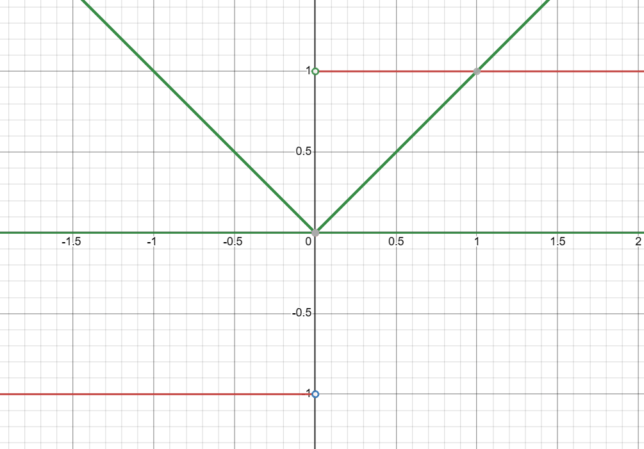
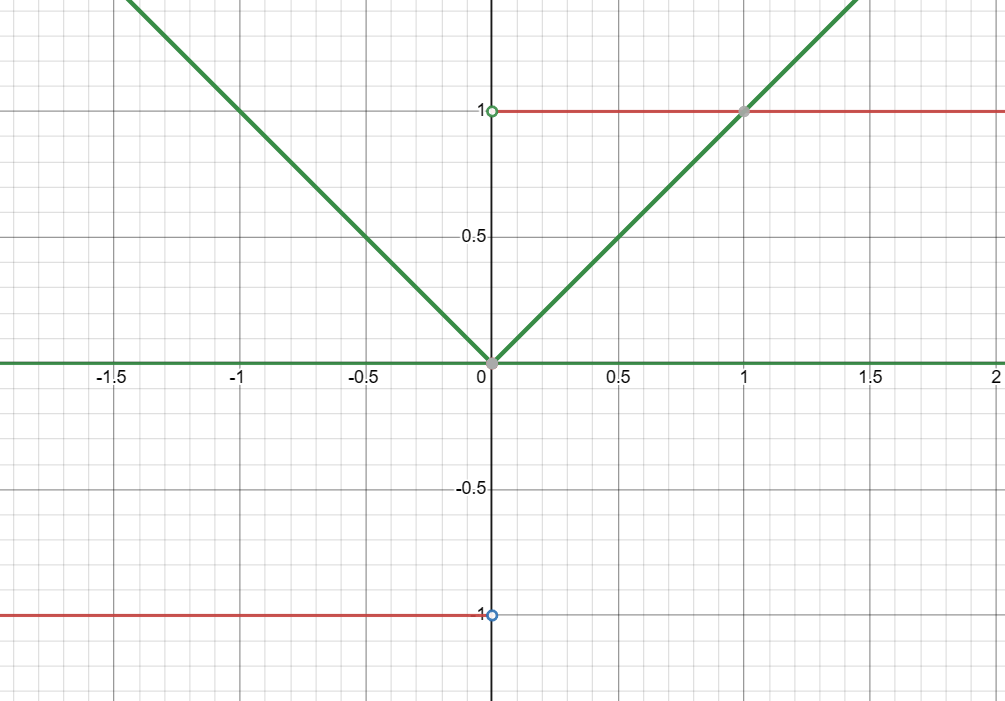
Graph Description: |x| with Holes at (0,1) and (0,-1)
Your graph illustrates the function \( |x| \) along with constant functions \( y = 1 \) and \( y = -1 \) on a coordinate plane.
Key Features:
- The main function \( |x| \) consists of two linear segments intersecting at the origin (0,0).
- For \( x \) values greater than or equal to 0, the graph of \( |x| \) coincides with the line \( y = x \).
- For \( x \) values less than 0, the graph of \( |x| \) coincides with the line \( y = -x \).
- There are two holes in the graph at points (0,1) and (0,-1).
- At the point (0,1), there’s an open circle, indicating that the function is not defined at \( x = 0 \) for \( y = 1 \).
- At the point (0,-1), there’s another open circle, indicating that the function is not defined at \( x = 0 \) for \( y = -1 \).
- Two horizontal lines on the graph represent constant functions: \( y = 1 \) and \( y = -1 \).
- These constant functions are not affected by changes in \( x \) because they are horizontal lines located above and below the origin, respectively.