Quick Guide to Finding the Domain of 1/(x-1)
- Set the denominator x-1 equal to zero.
- Solve for x, which gives x = 1.
- Exclude this value from the domain, as it makes the denominator zero.
Exploring the Limitless: The Domain of 1/(x-1)
Domain in Inequality Form: x < 1 or x > 1 (The domain is all x such that x is less than 1 or x is greater than 1)
Domain in Interval Notation: (-∞, 1) ∪ (1, ∞) (The domain is from negative infinity to 1, union, from 1 to positive infinity)
Domain in Set-builder Notation: { x ∈ ℝ : x ≠ 1 } (The domain is the set of all x in the real numbers such that x is not equal to 1)
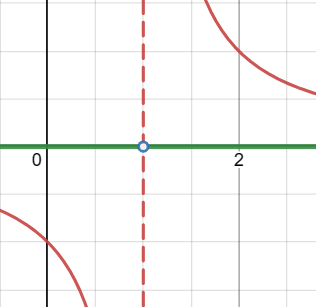
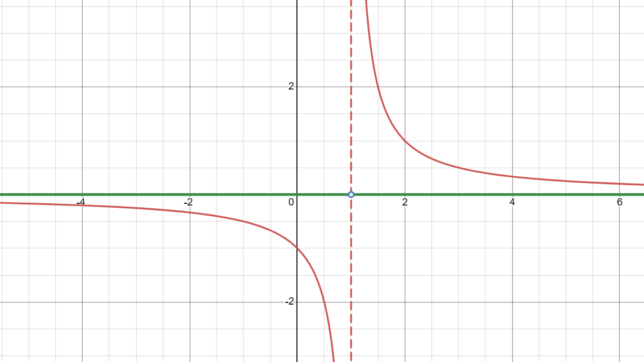
Visualizing the Graph of 1/(x-1)
- Vertical Asymptote: x = 1 (The graph approaches but never touches this line.)
- Horizontal Asymptote: y = 0 (The graph approaches but never reaches this line as x goes to positive or negative infinity.)
- Quadrants: The graph is in the 1st and 3rd quadrants, similar to 1/x but shifted one unit to the right.
- End Behavior: As x approaches 1 from the left, y approaches negative infinity. As x approaches 1 from the right, y approaches positive infinity.
