Solving Absolute Value Equations
To solve an equation involving absolute values, you need to consider different cases. Here’s a breakdown of the steps:
Original Equation
Given the equation: x² – 4|x| = 0, you need to consider two scenarios depending on the value of x:
- If x is greater than or equal to zero, the absolute value is just x.
- If x is less than zero, the absolute value becomes -x.
Case 1: x ≥ 0
Remove the absolute value to get: x² – 4x = 0. Factorize this to find the roots:
- Rewrite as x(x – 4) = 0.
- This leads to solutions: x = 0 and x = 4.
Case 2: x < 0
Rewriting with -x for the absolute value, you get: x² – 4(-x) = 0. This simplifies to:
- x² + 4x = 0.
- Factorize to get x(x + 4) = 0.
- The solutions in this case are: x = 0 and x = -4.
Common Solution
The common solution from both cases is x = 0, with additional solutions of x = 4 in Case 1 and x = -4 in Case 2.
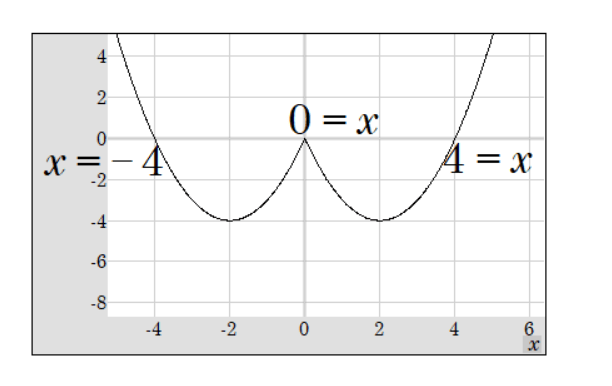
Graphical Interpretation of Quadratic Function with Absolute Value
This graph represents the function x² – 4|x|, showcasing how absolute values influence a quadratic expression. The curve has a unique shape, with important points along the x-axis indicating the roots of the equation.
X-Intercepts
The x-intercepts, where the graph crosses the x-axis, represent the solutions to the equation:
- x = -4
- x = 0
- x = 4
These values are derived from the original equation, considering both cases of absolute value.
Understanding the Graph
The “W” shape of the graph is a result of the absolute value operation. The left branch extends downward from x = -4, reaching a vertex before rising to cross the x-axis at x = 0. The right branch follows a similar pattern, descending to a vertex and then rising to cross the x-axis at x = 4. This pattern clearly demonstrates the effects of absolute value in quadratic functions.