Subtracting Two Vectors: A Comprehensive Guide

Keyphrase: Subtracting Two Vectors

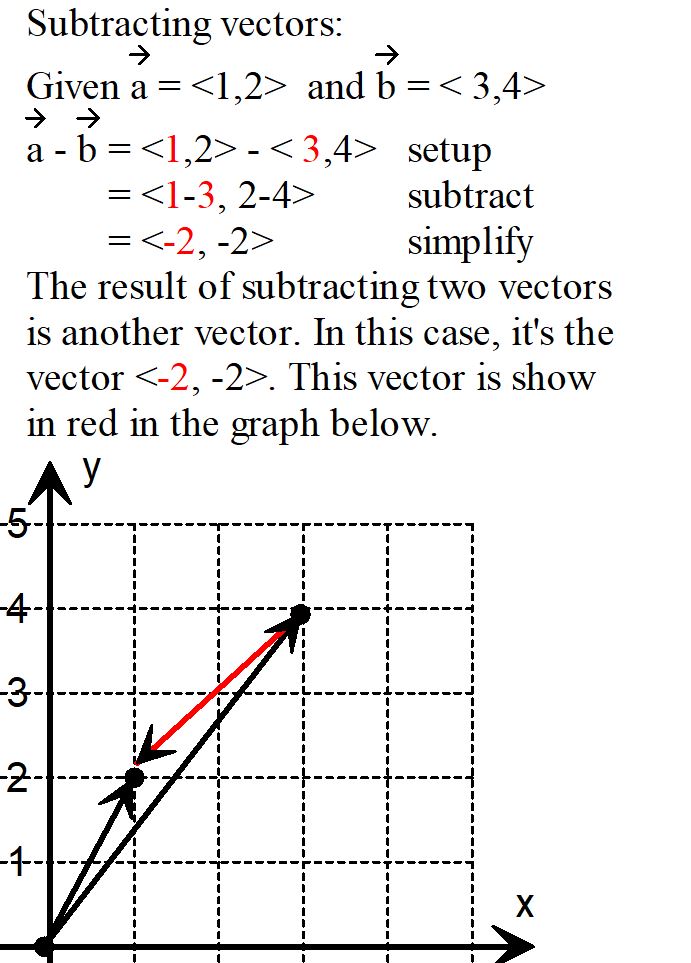
In this guide, we will explore the process of subtracting two vectors, specifically the vectors ⟨1,2⟩ and ⟨3,4⟩. Vector subtraction is a fundamental operation in mathematics, physics, and engineering, and understanding it is essential for various applications.

Steps to Subtract the Vectors ⟨1,2⟩ and ⟨3,4⟩:

1. Identify the Vectors: We have two vectors, ⟨1,2⟩ and ⟨3,4⟩, that we want to subtract.
2. Write the Subtraction Expression: The subtraction of the vectors is expressed as ⟨1,2⟩ – ⟨3,4⟩.
3. Subtract the Corresponding Components: Subtract the x-components and the y-components separately:
   • x-component: 1 – 3 = -2
   • y-component: 2 – 4 = -2
4. Write the Resulting Vector: The resulting vector after subtraction is ⟨-2,-2⟩.

Conclusion:

Subtracting Two Vectors, such as ⟨1,2⟩ and ⟨3,4⟩, involves subtracting the corresponding components of the vectors. The result of this subtraction is the new vector ⟨-2,-2⟩. This operation is widely used in physics to find relative displacement, in computer graphics to calculate direction, and in mathematics to perform geometric transformations. Understanding how to subtract vectors is a key skill in these fields.

Efficient Calculation:

Subtracting Two Vectors ⟨1,2⟩ and ⟨3,4⟩ can be efficiently calculated as: ⟨1,2⟩ – ⟨3,4⟩ = ⟨1 – 3, 2 – 4⟩ = ⟨-2, -2⟩.

Subtracting Two Vectors: A Comprehensive Guide

Keyphrase: Subtracting Two Vectors

In this guide, we will explore the process of subtracting two vectors, specifically the vectors ⟨5,7⟩ and ⟨2,3⟩. Vector subtraction is a fundamental operation in mathematics, physics, and engineering, and understanding it is essential for various applications.

Steps to Subtract the Vectors ⟨5,7⟩ and ⟨2,3⟩:

1. Identify the Vectors: We have two vectors, ⟨5,7⟩ and ⟨2,3⟩, that we want to subtract.
2. Write the Subtraction Expression: The subtraction of the vectors is expressed as ⟨5,7⟩ – ⟨2,3⟩.
3. Subtract the Corresponding Components: Subtract the x-components and the y-components separately:
   • x-component: 5 – 2 = 3
   • y-component: 7 – 3 = 4
4. Write the Resulting Vector: The resulting vector after subtraction is ⟨3,4⟩.

Conclusion:

Subtracting Two Vectors, such as ⟨5,7⟩ and ⟨2,3⟩, involves subtracting the corresponding components of the vectors. The result of this subtraction is the new vector ⟨3,4⟩. This operation is widely used in physics to find relative displacement, in computer graphics to calculate direction, and in mathematics to perform geometric transformations. Understanding how to subtract vectors is a key skill in these fields.

Efficient Calculation:

Subtracting Two Vectors ⟨5,7⟩ and ⟨2,3⟩ can be efficiently calculated as: ⟨5,7⟩ – ⟨2,3⟩ = ⟨5 – 2, 7 – 3⟩ = ⟨3, 4⟩.

Subtracting Two Vectors with Fractions: A Detailed Guide

Keyphrase: Subtracting Two Vectors with Fractions

In this guide, we will explore the process of subtracting two vectors with fractional components, specifically the vectors \( \left\langle \frac{1}{2}, \frac{3}{4} \right\rangle \) and \( \left\langle \frac{1}{3}, \frac{2}{3} \right\rangle \). Vector subtraction with fractions is a common operation in mathematics and physics, and understanding it is essential for various applications.

Steps to Subtract the Vectors \( \left\langle \frac{1}{2}, \frac{3}{4} \right\rangle \) and \( \left\langle \frac{1}{3}, \frac{2}{3} \right\rangle \):

1. Identify the Vectors: We have two vectors, \( \left\langle \frac{1}{2}, \frac{3}{4} \right\rangle \) and \( \left\langle \frac{1}{3}, \frac{2}{3} \right\rangle \), that we want to subtract.
2. Write the Subtraction Expression: The subtraction of the vectors is expressed as \( \left\langle \frac{1}{2}, \frac{3}{4} \right\rangle – \left\langle \frac{1}{3}, \frac{2}{3} \right\rangle \).
3. Subtract the Corresponding Components: Subtract the x-components and the y-components separately:
   • x-component: \( \frac{1}{2} – \frac{1}{3} = \frac{1}{6} \)
   • y-component: \( \frac{3}{4} – \frac{2}{3} = \frac{1}{12} \)
4. Write the Resulting Vector: The resulting vector after subtraction is \( \left\langle \frac{1}{6}, \frac{1}{12} \right\rangle \).

Conclusion:

Subtracting Two Vectors with Fractions, such as \( \left\langle \frac{1}{2}, \frac{3}{4} \right\rangle \) and \( \left\langle \frac{1}{3}, \frac{2}{3} \right\rangle \), involves subtracting the corresponding fractional components of the vectors. The result of this subtraction is the new vector \( \left\langle \frac{1}{6}, \frac{1}{12} \right\rangle \). This operation is essential in various mathematical and scientific contexts.

Efficient Calculation:

Subtracting Two Vectors with Fractions \( \left\langle \frac{1}{2}, \frac{3}{4} \right\rangle \) and \( \left\langle \frac{1}{3}, \frac{2}{3} \right\rangle \) can be efficiently calculated as: \( \left\langle \frac{1}{2}, \frac{3}{4} \right\rangle – \left\langle \frac{1}{3}, \frac{2}{3} \right\rangle = \left\langle \frac{1}{6}, \frac{1}{12} \right\rangle \).