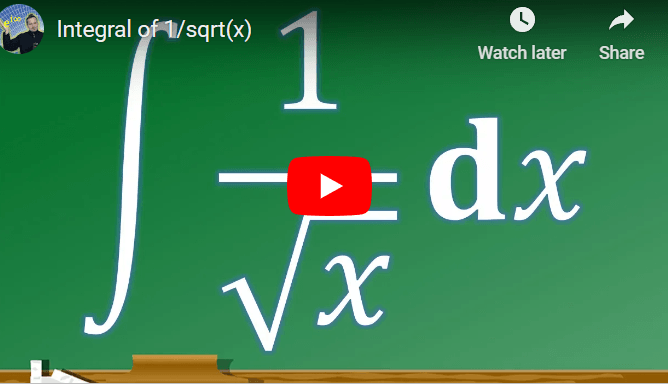Integral of 1/√x: A Detailed Step-by-Step Guide

Given Integral: ∫(1/√x) dx

Step 1: Rewrite the Integral

∫(1/√x) dx = ∫x^-1/2 dx (Rewriting 1/√x as x^-1/2)

Step 2: Apply the Power Rule for Integration

The power rule for integration states that ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C, where n ≠ -1.

Step 3: Substitute n = -1/2 into the Power Rule

∫x^-1/2 dx = (x^{-1/2 + 1})/(-1/2 + 1) + C (Substituting n = -1/2 into the power rule)

Step 4: Simplify the Exponent

(x^{-1/2 + 1})/(-1/2 + 1) = (x^1/2)/(1/2) + C (Simplifying the exponent -1/2 + 1 = 1/2)

Step 5: Simplify the Fraction

(x^1/2)/(1/2) = 2x^1/2 + C (Dividing by 1/2 is the same as multiplying by 2)

Step 6: Rewrite in Radical Form

2x^1/2 + C = 2√x + C (Rewriting x^1/2 as √x)

Conclusion: Final Result

The integral of 1/√x with respect to x is 2√x + C. This example demonstrates the application of the power rule for integration, simplification of exponents and fractions, and conversion between radical and exponential forms.

The image displays two curves on a coordinate plane. The first curve represents the function y = 1/√x, which is a decreasing curve that approaches the x-axis as x increases. It starts from the top left of the graph and gradually approaches the x-axis but never touches it. The second curve represents the integral of the first function, y = 2√x, which is an increasing curve that starts from the origin (0,0) and rises to the right. It forms a smooth, upward-opening parabolic shape. The graph illustrates the relationship between the original function and its integral, showing how the integral of a decreasing function can be an increasing function. Both curves are plotted for x values ranging from 0.1 to 10. The x and y axes are clearly labeled, and legends are provided to identify each curve.