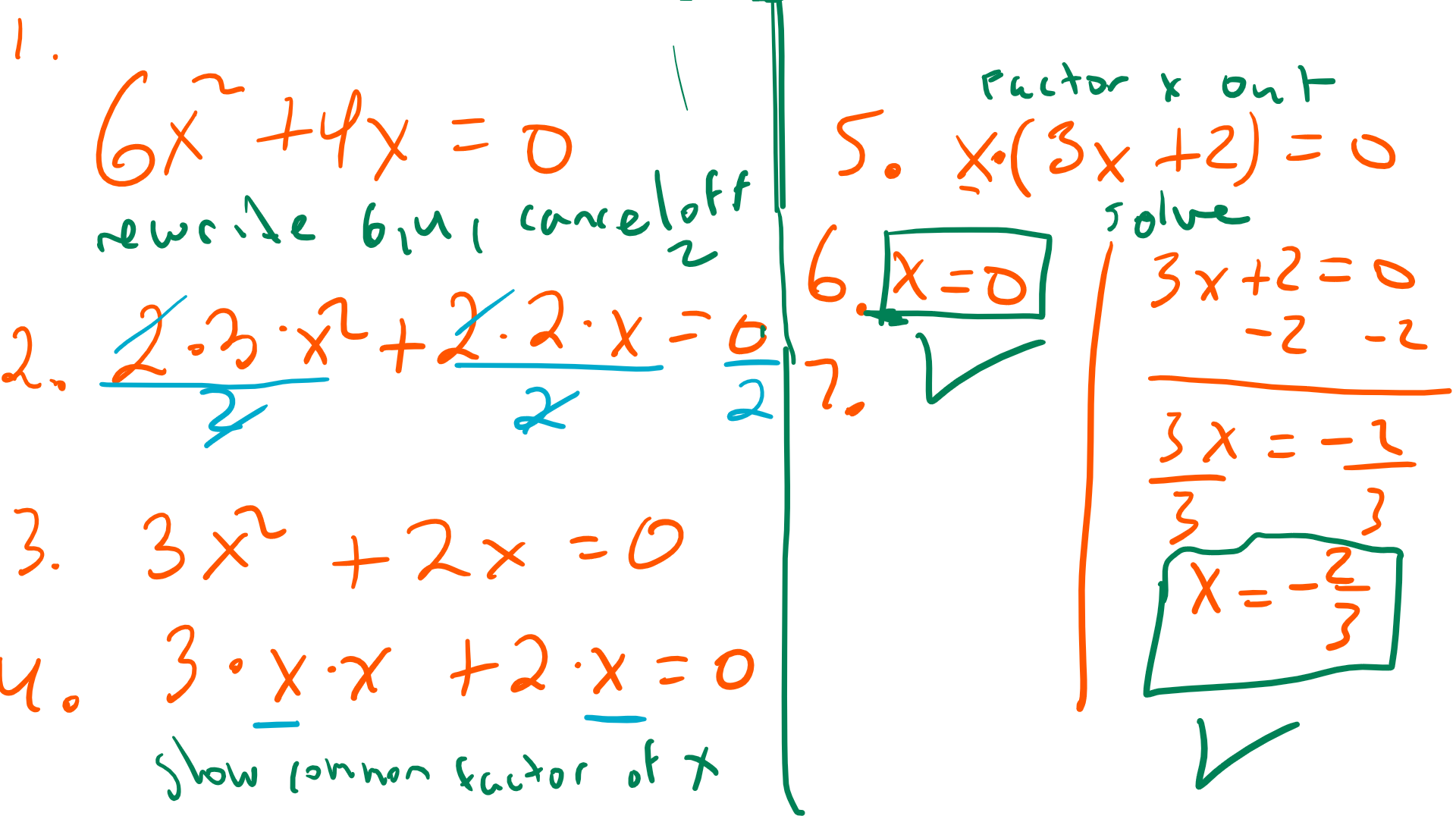Original Equation: 6x² + 4x = 0

1. Identify the Coefficients: Look at the coefficients of the terms: 6 and 4.

2. Find the GCF of the Coefficients: The GCF of 6 and 4 is 2. // Found by listing the factors of 6 (1, 2, 3, 6) and 4 (1, 2, 4) and identifying the largest common factor.

3. Identify the Common Variable Factor: Both terms have an x, so x is also a common factor.

4. Combine the Numeric and Variable Factors: The combined GCF is 2x.

5. Factor Out the GCF: Divide both terms by the GCF and write the equation as: 6x² + 4x = 2x(3x + 2) = 0 // Factored out 2x.

6. Set Each Factor Equal to Zero: Since the product of two numbers is zero if and only if at least one of the numbers is zero:

– 2x = 0 // Set the first factor equal to zero.

– 3x + 2 = 0 // Set the second factor equal to zero.

7. Solve for x:

– For 2x = 0: x = 0 // Divided by 2.

– For 3x + 2 = 0: 3x = -2 // Subtracted 2, then x = -2/3 // Divided by 3.

The solutions to the equation 6x² + 4x = 0 are x = 0 and x = -2/3. By identifying the GCF and factoring it out, we were able to simplify the equation and find the solutions.