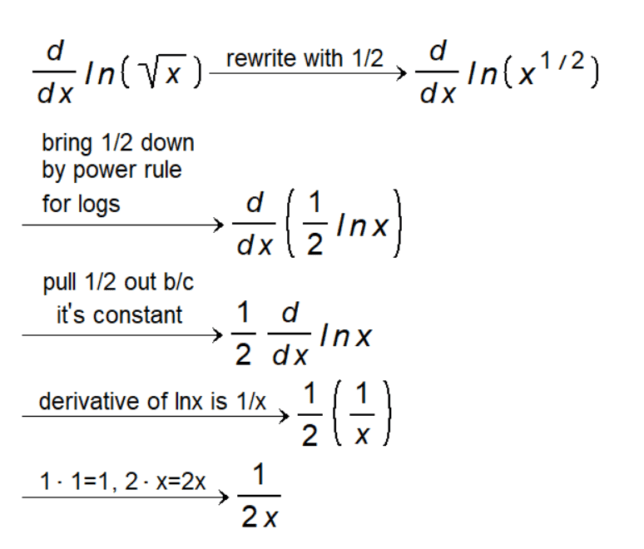Example: Finding the rate of change of \( \ln(\sqrt{x}) \)
Step 1: Start with the Original Expression
We have \( \ln(\sqrt{x}) \) and we want to find its rate of change.
Step 2: Rewrite Using Exponents
First, change \( \sqrt{x} \) to \( x^{\frac{1}{2}} \). So, the expression becomes \( \ln(x^{\frac{1}{2}}) \).
Step 3: Use Logarithmic Properties to Simplify
Bring down the exponent \( \frac{1}{2} \) to the front. Now, the expression is \( \frac{1}{2} \ln(x) \).
Step 4: Find the Rate of Change
We want to find how \( \frac{1}{2} \ln(x) \) changes as \( x \) changes. The rate of change of \( \ln(x) \) is \( \frac{1}{x} \).
Step 5: Multiply by \( \frac{1}{2} \)
Finally, we have \( \frac{1}{2} \) times \( \frac{1}{x} \), which simplifies to \( \frac{1}{2x} \).
Step 6: Final Answer
The rate of change of \( \ln(\sqrt{x}) \) is \( \frac{1}{2x} \).