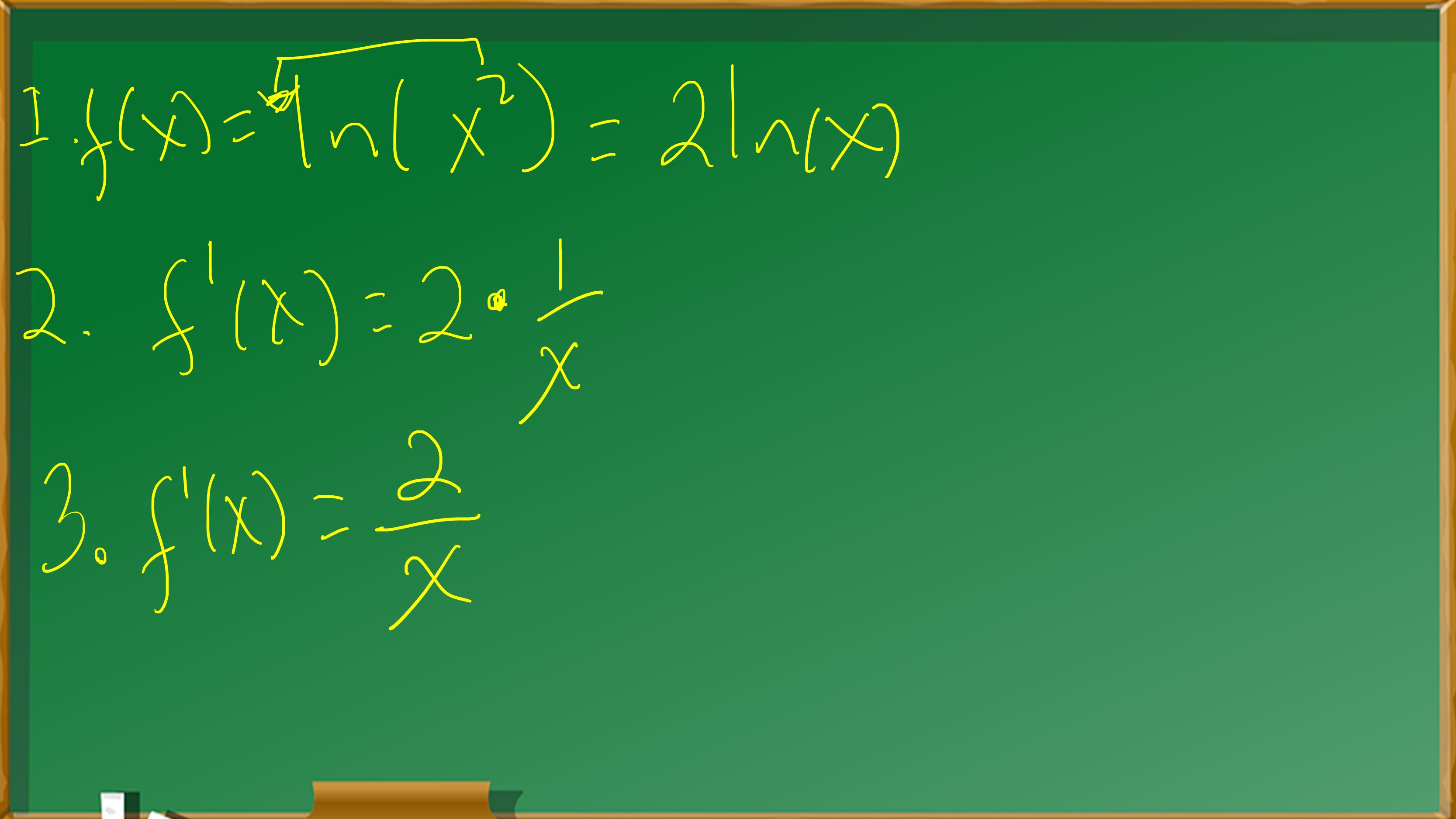
Detailed Differentiation of \( \ln(x^2) \) using the Chain Rule

Mathematical Steps	Explanation
Start with \( f(x) = \ln(x^2) \)	We begin with the function \( f(x) = \ln(x^2) \) that we want to differentiate.
Identify \( f(g(x)) \) and \( g(x) \)	\( f(g(x)) = \ln(g(x)) \) and \( g(x) = x^2 \)
Find \( f'(g(x)) \)	\( f'(g(x)) = \frac{1}{g(x)} = \frac{1}{x^2} \)
Find \( g'(x) \)	\( g'(x) = 2x \)
Apply the Chain Rule	\( \frac{d}{dx}[\ln(x^2)] = \frac{1}{x^2} \times 2x \)
Simplify	\( \frac{d}{dx}[\ln(x^2)] = \frac{2}{x} \)

Final Result

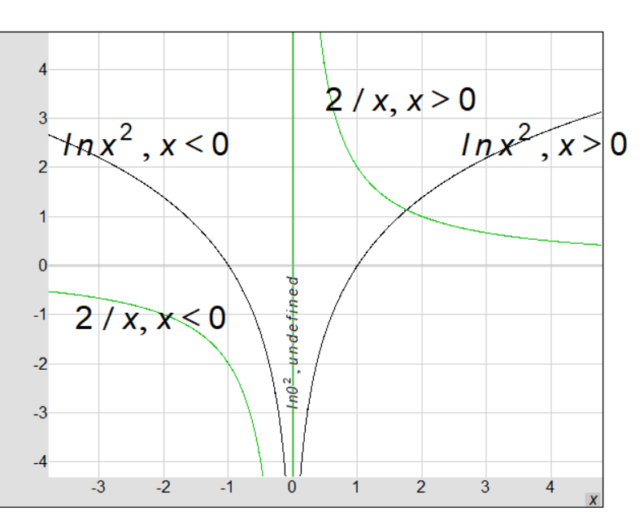
The derivative of \( \ln(x^2) \) is \( \frac{2}{x} \).