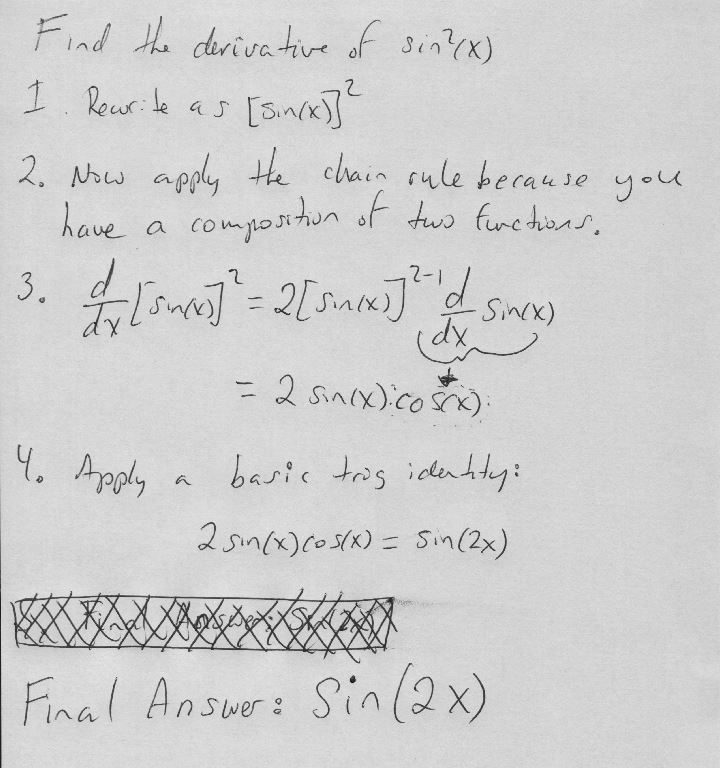Finding the Derivative of sin²(x)

Step 1: Recognize the Function

We are dealing with sin²(x), which can be written as (sin(x))².

Step 2: Use the Chain Rule

The chain rule states that d/dx[f(g(x))] = f'(g(x)) × g'(x).

Step 3: Differentiate (sin(x))²

The derivative of (sin(x))² with respect to x can be found using the chain rule:

d/dx[sin²(x)] = 2 × sin(x) × d/dx[sin(x)]

Step 4: Differentiate sin(x)

The derivative of sin(x) is cos(x).

Step 5: Combine the Terms

Combining all the terms, we get:

d/dx[sin²(x)] = 2 × sin(x) × cos(x)

Final Result

The derivative of sin²(x) with respect to x is 2 × sin(x) × cos(x).