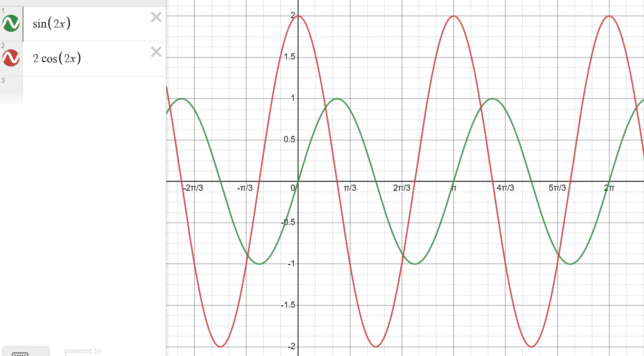
Example of a Trig Derivative: Derivative of sin(2x)

Given Function: f(x) = sin(2x)

Step 1: Apply the chain rule to differentiate sin(2x) with respect to x:

f'(x) = cos(2x) * (d/dx)(2x) (Using the chain rule: Derivative of sin(u) with respect to x is cos(u) * (du/dx))

f'(x) = cos(2x) * 2 (Derivative of 2x with respect to x is 2)

Step 2: Simplify the derivative to obtain the final result:

f'(x) = 2cos(2x)

Conclusion: The derivative of the function f(x) = sin(2x) with respect to x is f'(x) = 2cos(2x). This example demonstrates the application of the chain rule to find the derivative of a trigonometric function.

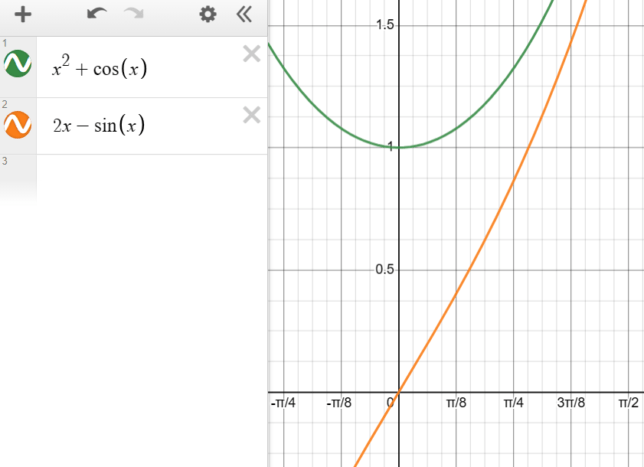
Example of a Trig Derivative: Derivative of x² + cos(x)

Given Function: f(x) = x² + cos(x)

Step 1: Calculate the derivative of x² using the power rule:

\(\frac{d}{dx}(x^2) = 2x^{2-1} = 2x\) (Applying the power rule: Multiply the exponent by the coefficient)

Step 2: Calculate the derivative of cos(x) using the derivative of cos(x) rule:

\(\frac{d}{dx}(\cos(x)) = -\sin(x)\) (Using the derivative of cos(x) rule: Derivative of cos(x) is -sin(x))

Step 3: Combine the derivatives of x² and cos(x) to find the derivative of the entire function:

\(\frac{d}{dx}(x^2 + \cos(x)) = 2x – \sin(x)\) (Combining the derivatives using the sum rule)

Example of a Trig Derivative: Derivative of x² + sin(2x)

Given Function: f(x) = x² + sin(2x)

Step 1: Differentiate \(x²\) with respect to \(x\) using the power rule:

f'(x) = 2x²⁻¹ = 2x

Step 2: Apply the chain rule to differentiate \(sin(2x)\) with respect to \(x\):

f'(x) = 2x + cos(2x) * d/dx(2x) (Using the chain rule: Derivative of \(sin(u)\) with respect to \(x\) is \(cos(u) * du/dx\)

f'(x) = 2x + cos(2x) * 2 (Derivative of \(2x\) with respect to \(x\) is 2)

Step 3: Simplify the derivative to obtain the final result:

f'(x) = 2x + 2cos(2x)

Conclusion: The derivative of the function \(f(x) = x² + sin(2x)\) with respect to \(x\) is \(f'(x) = 2x + 2cos(2x)\). This example demonstrates the application of the power rule and the chain rule to find the derivative of a function that includes a trigonometric term.

Example of a Trig Derivative: Derivative of sin(x) + cos(3x)

Given Function: f(x) = sin(x) + cos(3x)

Step 1: Differentiate the first term, sin(x), with respect to x:

The derivative of sin(x) with respect to x is cos(x).

Step 2: Differentiate the second term, cos(3x), with respect to x:

Apply the chain rule: The derivative of cos(u) where u = 3x is -sin(u), and the derivative of u with respect to x is 3.

The derivative of cos(3x) with respect to x is -3sin(3x).

Step 3: Combine the derivatives of both terms:

f'(x) = cos(x) – 3sin(3x)

Conclusion: The derivative of the function f(x) = sin(x) + cos(3x) with respect to x is f'(x) = cos(x) – 3sin(3x). This example demonstrates the application of basic trigonometric derivatives and the chain rule.

Example of a Trig Derivative: Derivative of tan(x) – sin(2x)

Given Function: f(x) = tan(x) – sin(2x)

Step 1: Differentiate the first term, tan(x), with respect to x:

The derivative of tan(x) with respect to x is sec²(x).

Step 2: Differentiate the second term, sin(2x), with respect to x:

Apply the chain rule: The derivative of sin(u) where u = 2x is cos(u), and the derivative of u with respect to x is 2.

The derivative of sin(2x) with respect to x is 2cos(2x).

Step 3: Combine the derivatives of both terms:

f'(x) = sec²(x) – 2cos(2x)

Conclusion: The derivative of the function f(x) = tan(x) – sin(2x) with respect to x is f'(x) = sec²(x) – 2cos(2x). This example demonstrates the application of basic trigonometric derivatives and the chain rule to find the derivative of a function that includes a tangent term and a sine term with a coefficient inside the argument.

Example of a Trig Derivative: Derivative of cos(3x) + sin(x/2)

Given Function: f(x) = cos(3x) + sin(x/2)

Step 1: Differentiate the first term, cos(3x), with respect to x:

Apply the chain rule: The derivative of cos(u) where u = 3x is -sin(u), and the derivative of u with respect to x is 3.

The derivative of cos(3x) with respect to x is -3sin(3x).

Step 2: Differentiate the second term, sin(x/2), with respect to x:

Apply the chain rule: The derivative of sin(u) where u = x/2 is cos(u), and the derivative of u with respect to x is 1/2.

The derivative of sin(x/2) with respect to x is (1/2)cos(x/2).

Step 3: Combine the derivatives of both terms:

f'(x) = -3sin(3x) + (1/2)cos(x/2)

Conclusion: The derivative of the function f(x) = cos(3x) + sin(x/2) with respect to x is f'(x) = -3sin(3x) + (1/2)cos(x/2). This example demonstrates the application of basic trigonometric derivatives and the chain rule to find the derivative of a function that includes a cosine term with a coefficient inside the argument and a sine term with a fraction inside the argument.

Example of a Trig Derivative: Derivative of sin(4x) – cos(3x/2)

Given Function: f(x) = sin(4x) – cos(3x/2)

Step 1: Differentiate the first term, sin(4x), with respect to x:

Apply the chain rule: The derivative of sin(u) where u = 4x is cos(u), and the derivative of u with respect to x is 4.

The derivative of sin(4x) with respect to x is 4cos(4x).

Step 2: Differentiate the second term, cos(3x/2), with respect to x:

Apply the chain rule: The derivative of cos(u) where u = 3x/2 is -sin(u), and the derivative of u with respect to x is 3/2.

The derivative of cos(3x/2) with respect to x is -(3/2)sin(3x/2).

Step 3: Combine the derivatives of both terms:

f'(x) = 4cos(4x) – (3/2)sin(3x/2)

Conclusion: The derivative of the function f(x) = sin(4x) – cos(3x/2) with respect to x is f'(x) = 4cos(4x) – (3/2)sin(3x/2). This example demonstrates the application of basic trigonometric derivatives and the chain rule to find the derivative of a function that includes a sine term with a coefficient inside the argument and a cosine term with a fraction inside the argument.