Step	Expression	Explanation
1	d/dx e⁻ˣ	Start with the original expression
2	e⁻ˣ d/dx (-x)	Apply the chain rule: derivative of the outer function times derivative of the inner function
3	d/dx (-x) = -1	Find the derivative of the inner function -x
4	-e⁻ˣ	Combine the derivatives

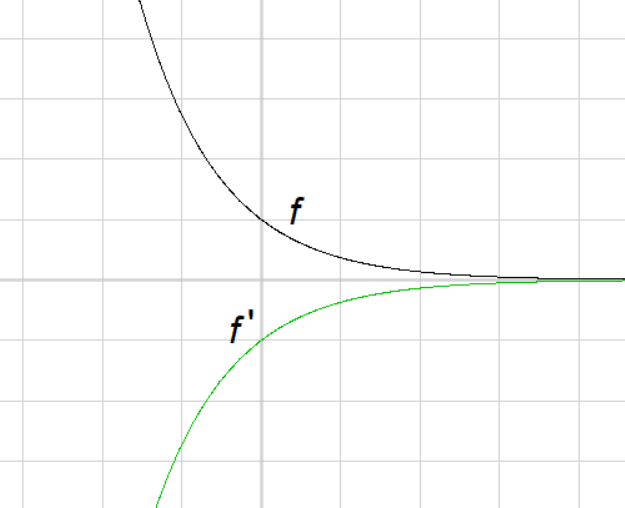
The relationship between the function \( f(x) = e^{-x} \) and its derivative \( f'(x) = -e^{-x} \) is such that the y-coordinate of the graph of \( f'(x) = -e^{-x} \) at any point \( x \) gives the slope of the tangent line to the graph of \( f(x) = e^{-x} \) at that same point \( x \). In other words, the graph of \( -e^{-x} \) visually represents how the slope of the graph of \( e^{-x} \) is changing as \( x \) varies.