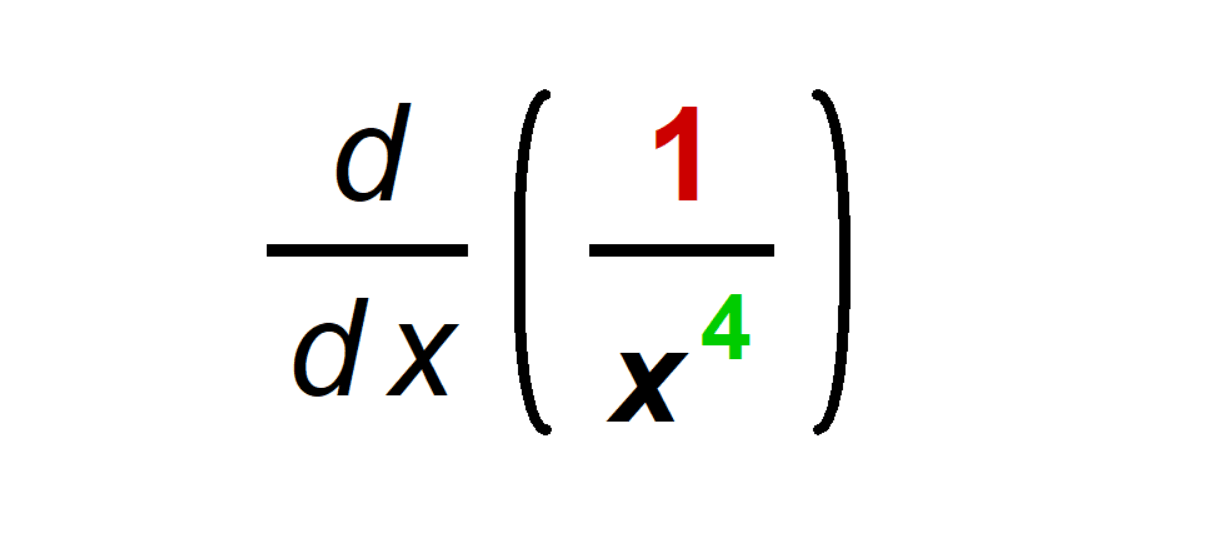Unveiling the Derivative of 1/x²: A Mathematical Exploration

Understanding the Function: The function f(x) = 1/x² represents a fascinating mathematical relationship where the output is the reciprocal of the square of the input. It’s a curve that diminishes rapidly as x moves away from 0.

Rewriting with Negative Exponents: To facilitate differentiation, we rewrite the function using negative exponents. This transformation retains the function’s essence but presents it in a form ready for differentiation:

f(x) = x⁻²

Applying the Power Rule: Utilizing the power rule, a cornerstone of calculus, we multiply by the exponent and then subtract 1 from the exponent:

f'(x) = (-2)x⁻²⁻¹ = -2x⁻³

Interpreting the Negative Exponent: The negative exponent in our result, -2x⁻³, signifies that the variable x is in the denominator. It’s a vivid depiction of the function’s rapid change near x = 0.

Converting Back to Positive Exponent: For clarity, we convert the negative exponent back to a positive exponent in the denominator:

f'(x) = -2/x³

Final Interpretation: The derivative -2/x³ encapsulates the behavior of the original function 1/x², revealing how it changes as x varies. The negative sign and the x³ in the denominator together paint a picture of a function that decreases swiftly, especially near x = 0.

Thus, the derivative of 1/x² is -2/x³, a result that not only solves a mathematical problem but also invites us to delve deeper into the intriguing world of calculus.

Unlocking the Derivative of 1/x⁴: A Deep Dive into Calculus

Understanding the Function: The function f(x) = 1/x⁴ is a captivating mathematical expression where the output is the reciprocal of the fourth power of the input. This curve decreases even more rapidly than 1/x² as x moves away from 0.

Rewriting with Negative Exponents: To set the stage for differentiation, we rewrite the function using negative exponents. This transformation maintains the function’s meaning but prepares it for differentiation:

f(x) = x⁻⁴

Applying the Power Rule: The power rule is our key to unlocking the derivative. We multiply by the exponent and then subtract 1 from the exponent:

f'(x) = (-4)x⁻⁴⁻¹ = -4x⁻⁵

Interpreting the Negative Exponent: The negative exponent in our result, -4x⁻⁵, tells us that the variable x is in the denominator. It’s a mathematical signature of the function’s swift change near x = 0.

Converting Back to Positive Exponent: For ease of understanding, we convert the negative exponent back to a positive exponent in the denominator:

f'(x) = -4/x⁵

Final Interpretation: The derivative -4/x⁵ encapsulates the behavior of the original function 1/x⁴. The negative sign and the x⁵ in the denominator together illustrate a function that decreases at an incredibly rapid pace, especially near x = 0.

Thus, the derivative of 1/x⁴ is -4/x⁵, a result that not only answers a mathematical question but also opens a window into the elegant world of calculus.