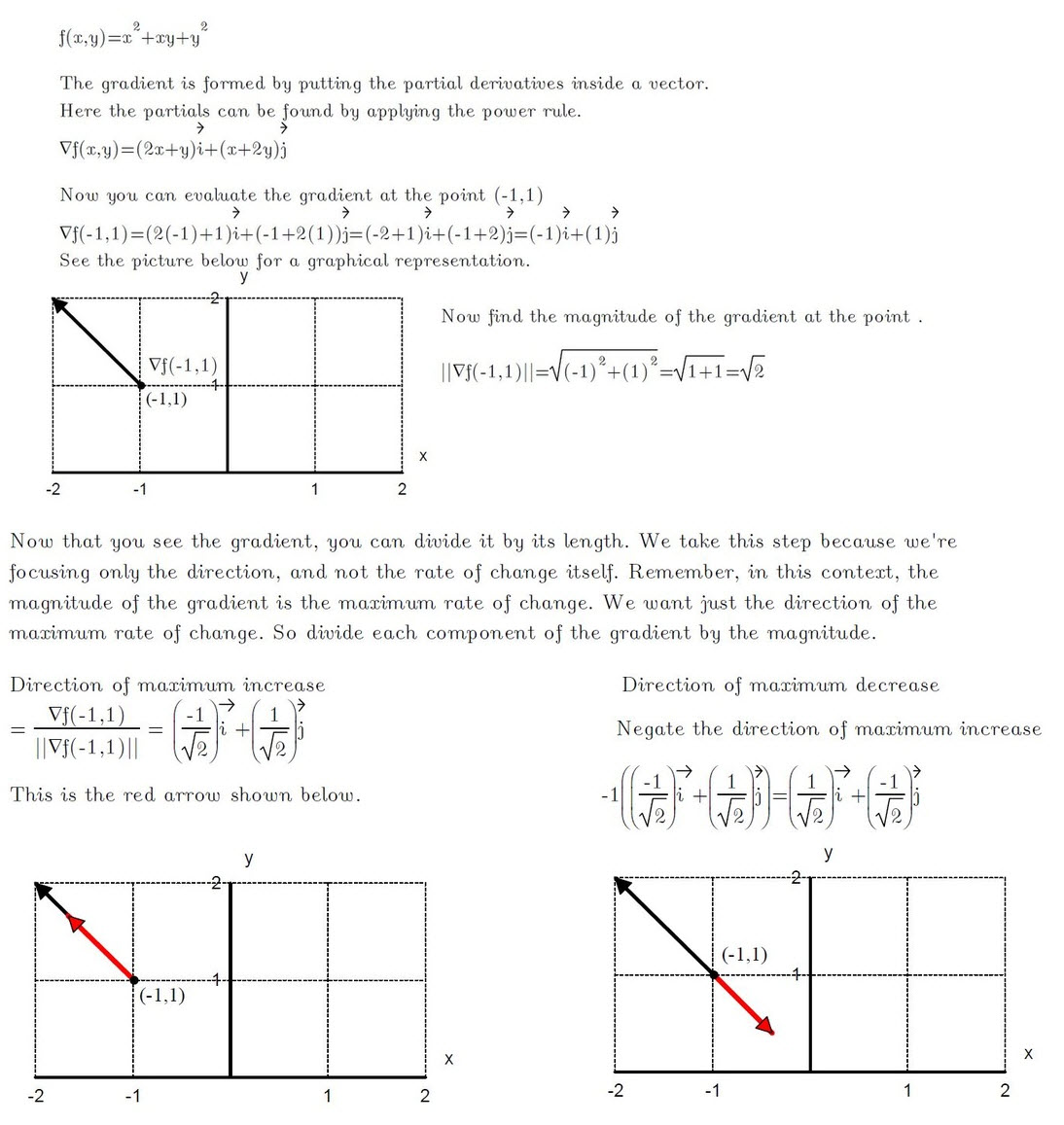
Understanding the Gradient of f(x,y) = x² + xy + y²

The gradient of a function gives us the direction and rate of the steepest ascent. For the function f(x,y) = x² + xy + y², we can calculate the gradient as follows:

Partial Derivative with respect to x: ∂f/∂x = 2x + y

Partial Derivative with respect to y: ∂f/∂y = x + 2y

The gradient is then given by the vector: ∇f = (2x + y, x + 2y)

This vector points in the direction of the steepest ascent of the function and its magnitude represents the rate of change in that direction.

For a detailed visualization of the gradient and how it behaves at various points on the surface of the function, please refer to the image below.

The image illustrates the gradient of a function, depicted as a blue line. The x-axis symbolizes the input variable, and the y-axis shows the gradient. The point (-1,1) is highlighted, with the gradient at this point represented by a red arrow. The magnitude of the gradient is -2, indicating a decrease at this rate. The red arrow also signifies the direction of maximum increase, with a magnitude of 2, while the opposite direction indicates the maximum decrease.