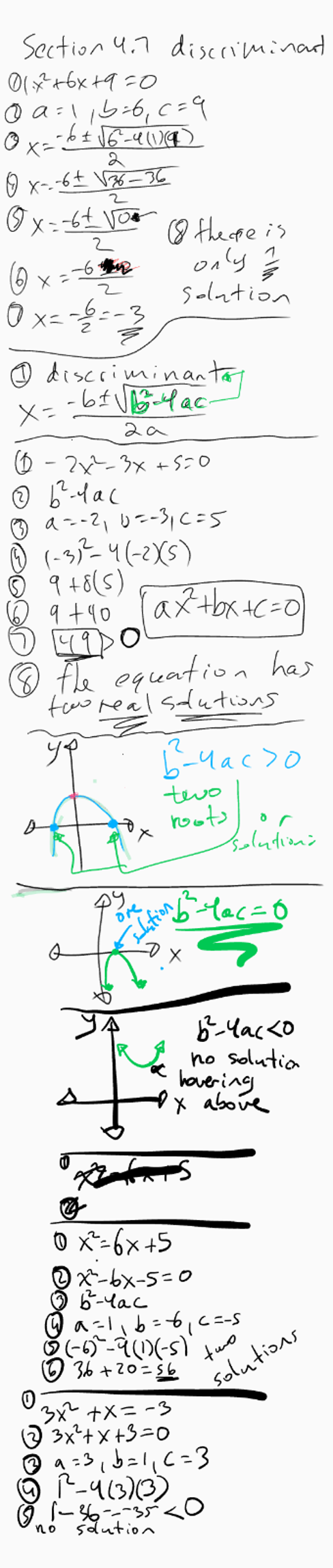
Quadratic Equation: x² + 6x + 9 = 0

Step 1: Identify Coefficients

a = 1, b = 6, c = 9 | Coefficients for the standard form of a quadratic equation ax² + bx + c = 0.

Step 2: Calculate the Discriminant

D = b² – 4ac | Formula for the discriminant of a quadratic equation.

D = (6)² – 4(1)(9) | Substitute the values of a, b, and c into the formula.

D = 36 – 36 | Square 6 to get 36, then multiply 4 by 1 and 9 to get 36.

D = 0 | Subtract 36 from 36 to find the value of the discriminant.

Step 3: Analyze the Discriminant

D = 0 | Since the discriminant is zero, the quadratic equation has exactly one real solution.

Summary: The discriminant of the quadratic equation x² + 6x + 9 = 0 is zero, indicating that the equation has exactly one real solution. This occurs when the parabola represented by the equation touches the x-axis at a single point.

Quadratic Equation: -2x² – 3x + 5 = 0

Step 1: Identify Coefficients

a = -2, b = -3, c = 5 | Coefficients for the standard form of a quadratic equation ax² + bx + c = 0.

Step 2: Calculate the Discriminant

D = b² – 4ac | Formula for the discriminant of a quadratic equation.

D = (-3)² – 4(-2)(5) | Substitute the values of a, b, and c into the formula.

D = 9 + 40 | Square -3 to get 9, then multiply 4 by -2 and 5 to get 40.

D = 49 | Add 9 and 40 to find the value of the discriminant.

Step 3: Analyze the Discriminant

D = 49 | Since the discriminant is greater than zero, the quadratic equation has two distinct real solutions.

Summary: The discriminant of the quadratic equation -2x² – 3x + 5 = 0 is 49, indicating that the equation has two distinct real solutions. This occurs when the parabola represented by the equation intersects the x-axis at two distinct points.

Given Equation: x² = 6x + 5

Step 1: Rearrange to Standard Form

x² = 6x + 5 | Original equation.

x² – 6x – 5 = 0 | Subtract 6x and 5 from both sides to get standard form ax² + bx + c = 0.

Step 2: Identify Coefficients

a = 1, b = -6, c = -5 | Coefficients for the standard form of a quadratic equation ax² + bx + c = 0.

Step 3: Calculate the Discriminant

D = b² – 4ac | Formula for the discriminant of a quadratic equation.

D = (-6)² – 4(1)(-5) | Substitute the values of a, b, and c into the formula.

D = 36 + 20 | Square -6 to get 36, then multiply 4 by 1 and -5 to get 20.

D = 56 | Add 36 and 20 to find the value of the discriminant.

Step 4: Analyze the Discriminant

D = 56 | Since the discriminant is greater than zero, the quadratic equation has two distinct real solutions.

Summary: The discriminant of the rearranged quadratic equation x² – 6x – 5 = 0 is 56, indicating that the equation has two distinct real solutions. This occurs when the parabola represented by the equation intersects the x-axis at two distinct points.

Given Equation: 3x² + x = 3

Step 1: Rearrange to Standard Form

3x² + x = 3 | Original equation.

3x² + x – 3 = 0 | Subtract 3 from both sides to get standard form ax² + bx + c = 0.

Step 2: Identify Coefficients

a = 3, b = 1, c = -3 | Coefficients for the standard form of a quadratic equation ax² + bx + c = 0.

Step 3: Calculate the Discriminant

D = b² – 4ac | Formula for the discriminant of a quadratic equation.

D = (1)² – 4(3)(-3) | Substitute the values of a, b, and c into the formula.

D = 1 + 36 | Square 1 to get 1, then multiply 4 by 3 and -3 to get 36.

D = 37 | Add 1 and 36 to find the value of the discriminant.

Step 4: Analyze the Discriminant

D = 37 | Since the discriminant is greater than zero, the quadratic equation has two distinct real solutions.

Summary: The discriminant of the rearranged quadratic equation 3x² + x – 3 = 0 is 37, indicating that the equation has two distinct real solutions. This occurs when the parabola represented by the equation intersects the x-axis at two distinct points.

Comparison of Discriminants:

D < 0 (3x² + x + 10): No real solutions (blue curve).

D > 0 (x² – 4x): Two distinct real solutions (orange curve).

D = 0 (x² – 4x + 4): Exactly one real solution (green curve).

Graph:

The blue curve represents the equation y = 3x² + x + 10, which has a discriminant less than zero, indicating no real solutions. The orange curve represents the equation y = x² – 4x, which has a discriminant greater than zero, indicating two distinct real solutions. The green curve represents the equation y = x² – 4x + 4, which has a discriminant equal to zero, indicating exactly one real solution.

This graph illustrates how the discriminant of a quadratic equation determines the nature of its solutions, with the blue curve showing no intersections with the x-axis, the orange curve showing two intersections, and the green curve showing one intersection.