Exploring Inequalities: Solving 3x – 4 < 2x + 5
Inequalities are like equations but with less strict conditions. Let’s solve this inequality step by step:
Step 1: Subtract 2x from both sides to get the x terms on one side:
3x – 2x – 4 < 2x – 2x + 5
x – 4 < 5
Step 2: Add 4 to both sides to isolate x:
x – 4 + 4 < 5 + 4
x < 9
The solution to the inequality 3x – 4 < 2x + 5 is x < 9. This means that the inequality holds for any value of x that is less than 9.
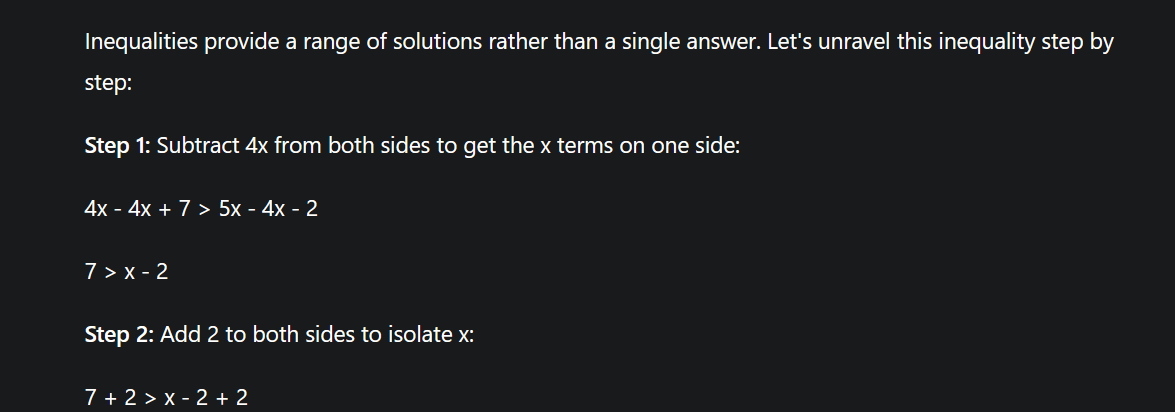
Mastering Inequalities: Solving 4x + 7 > 5x – 2
Inequalities provide a range of solutions rather than a single answer. Let’s unravel this inequality step by step:
Step 1: Subtract 4x from both sides to get the x terms on one side:
4x – 4x + 7 > 5x – 4x – 2
7 > x – 2
Step 2: Add 2 to both sides to isolate x:
7 + 2 > x – 2 + 2
9 > x
The solution to the inequality 4x + 7 > 5x – 2 is x < 9. This means that the inequality holds for any value of x that is less than 9.
Delving into Inequalities: A Detailed Guide to Solving 6x – 3 ≥ 4x + 9
Inequalities offer a rich understanding of mathematical relationships. Let’s dissect this inequality with precision:
Step 1: Gather Like Terms
Subtract 4x from both sides to get the x terms on one side:
6x – 4x – 3 ≥ 4x – 4x + 9
2x – 3 ≥ 9
Step 2: Isolate the Variable
Add 3 to both sides to move the constant term:
2x – 3 + 3 ≥ 9 + 3
2x ≥ 12
Step 3: Solve for x
Divide both sides by 2 to solve for x:
2x / 2 ≥ 12 / 2
x ≥ 6
Conclusion: The solution to the inequality 6x – 3 ≥ 4x + 9 is x ≥ 6. This means that the inequality holds for any value of x that is greater than or equal to 6. It’s a fascinating glimpse into how inequalities encapsulate a range of possibilities, reflecting the diverse and interconnected nature of mathematics.
Embark on a Mathematical Journey: Unraveling the Inequality 4x + 1 > 2x – 3
Are you ready to dive into the world of inequalities? Let’s unlock the secrets of the inequality 4x + 1 > 2x – 3, a mathematical expression that holds a universe of possibilities. Follow me on this exciting adventure:
Step 1: Unite the Variables
Subtract 2x from both sides to bring the x terms together. It’s the first step towards clarity:
4x – 2x + 1 > 2x – 2x – 3
2x + 1 > -3
Step 2: Free the Variable
Subtract 1 from both sides to liberate x from the constant. Feel the equation becoming simpler:
2x + 1 – 1 > -3 – 1
2x > -4
Step 3: Reveal the Solution
Divide both sides by 2 to unveil the value of x. The truth is near:
2x / 2 > -4 / 2
x > -2
Conclusion: The solution to the inequality 4x + 1 > 2x – 3 is x > -2. It’s not just a solution; it’s a testament to the elegance and power of mathematics. The inequality holds for any value of x that is greater than -2, opening a door to infinite possibilities. Embrace the beauty of inequalities and let them inspire you to explore further. The world of mathematics awaits, filled with wonder and discovery.