Translating Inequality to Interval Notation: x < a

Step 1: Understanding the Inequality Symbol <

The symbol < means 'less than,' and it corresponds to the open parenthesis ( in interval notation. The open parenthesis indicates that the endpoint a is not included in the interval.

Step 2: Understanding Negative Infinity -∞

The symbol -∞ represents negative infinity, which is always exclusive in interval notation. This means that the interval extends indefinitely in the negative direction but does not include negative infinity itself.

Step 3: Understanding the Upper Bound a

The symbol a is the upper bound of the interval. Because the inequality is x < a, the value a is not included in the interval, which is why we use an open parenthesis ( next to it.

Summary

Putting it all together, the inequality x < a translates to the interval notation ( -∞, a ).

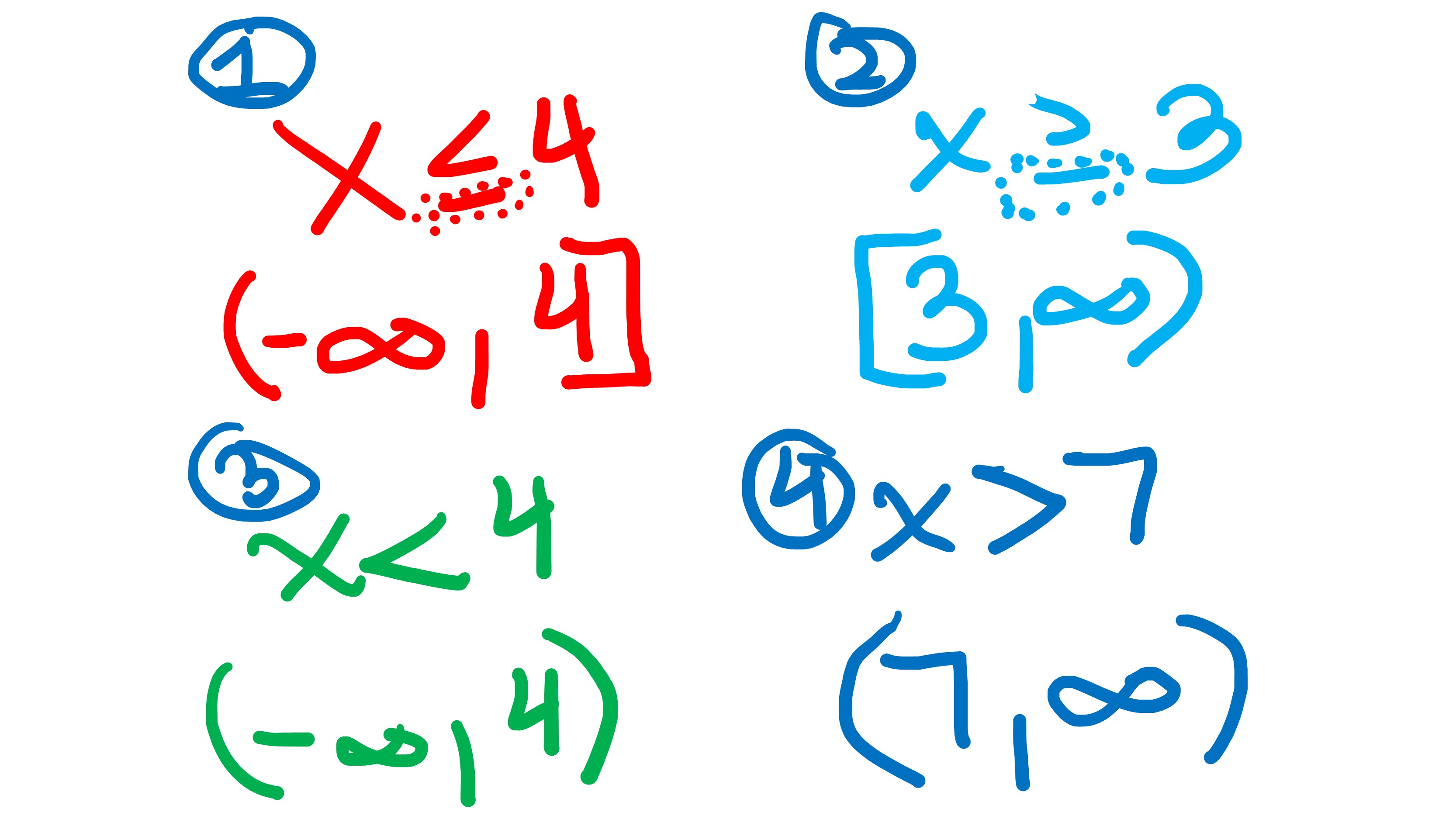
Translating Inequality to Interval Notation: x ≤ a

Step 1: Understanding the Inequality Symbol ≤

The symbol ≤ is a compound symbol that means ‘less than or equal to.’ The ‘less than’ part corresponds to the open parenthesis ( at the beginning of the interval, and the ‘equal to’ part corresponds to the closed bracket ] at the end of the interval.

Step 2: Understanding Negative Infinity -∞

The symbol -∞ represents negative infinity, which is always exclusive in interval notation. This means that the interval extends indefinitely in the negative direction but does not include negative infinity itself.

Step 3: Understanding the Upper Bound a

The symbol a is the upper bound of the interval. Because the inequality is x ≤ a, the value a is included in the interval, which is why we use a closed bracket ] next to it.

Summary

Putting it all together, the inequality x ≤ a translates to the interval notation ( -∞, a ].

Translating Inequality to Interval Notation: x ≥ a

Step 1: Understanding the Inequality Symbol ≥

The symbol ≥ is a compound symbol that means ‘greater than or equal to.’ The ‘greater than’ part corresponds to the open parenthesis ( at the end of the interval, and the ‘equal to’ part corresponds to the closed bracket [ at the beginning of the interval.

Step 2: Understanding Positive Infinity ∞

The symbol ∞ represents positive infinity, which is always exclusive in interval notation. This means that the interval extends indefinitely in the positive direction but does not include positive infinity itself.

Step 3: Understanding the Lower Bound a

The symbol a is the lower bound of the interval. Because the inequality is x ≥ a, the value a is included in the interval, which is why we use a closed bracket [ next to it.

Summary

Putting it all together, the inequality x ≥ a translates to the interval notation [ a, ∞ ).