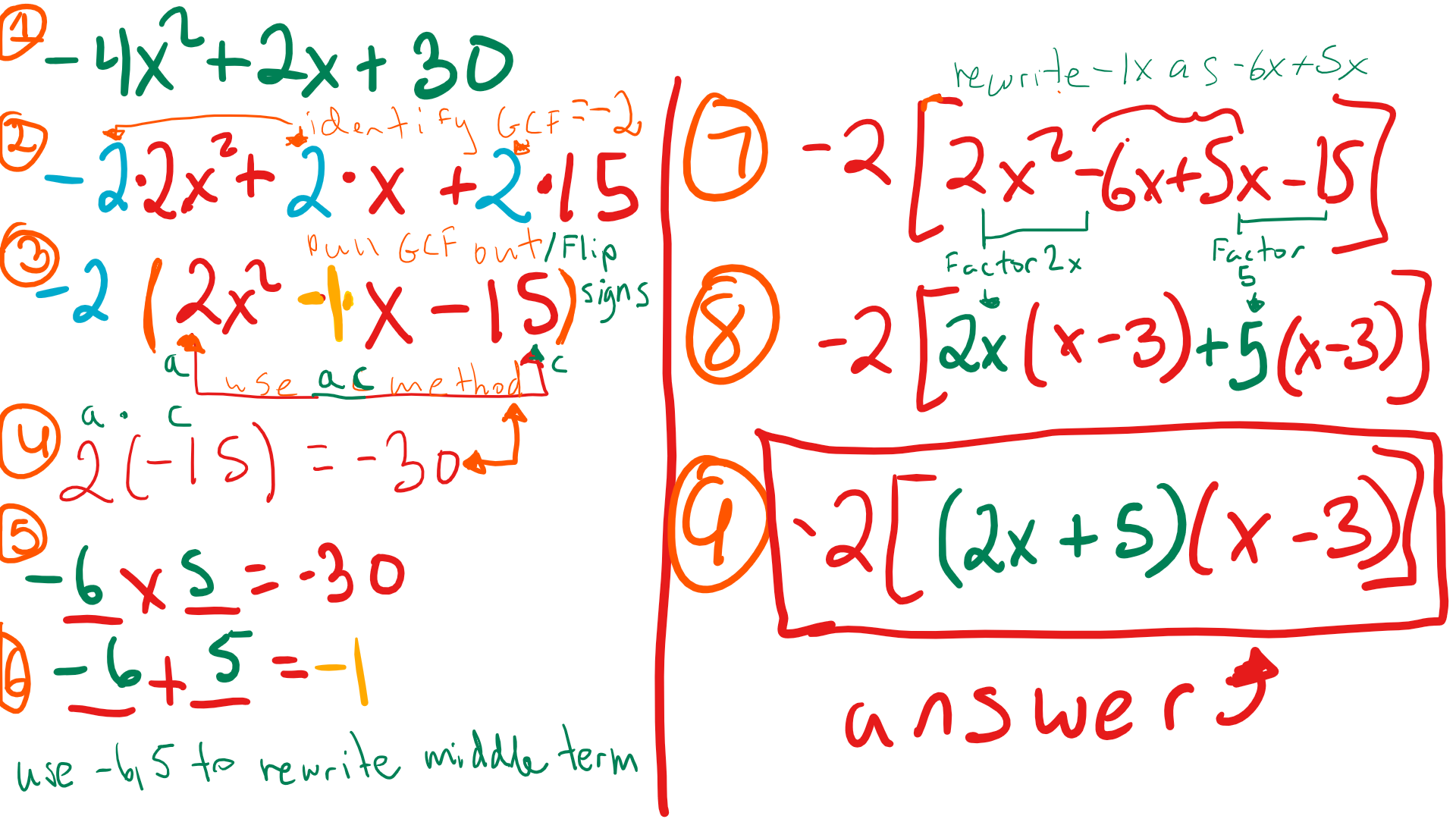Original Expression: -4x² + 2x + 30 // Given expression
Step 1: Factor out the GCF, which is -2: -2(2x² – x – 15) // Factoring out the GCF
Step 2: Focus on the trinomial 2x² – x – 15:
a. Identify the coefficients: a = 2, b = -1, c = -15 // Coefficients of the trinomial
b. Multiply a and c in the trinomial ax² + bx + c: 2 * (-15) = -30 // Finding the product ac
c. Find two numbers whose product is ac (-30) and sum is b (-1): -6 and 5 // Finding the numbers
d. Split the middle term using the numbers: 2x² – 6x + 5x – 15 // Splitting the middle term
e. Group the terms: (2x² – 6x) + (5x – 15) // Grouping the terms
f. Factor out the GCF from each group: 2x(x – 3) + 5(x – 3) // Factoring the groups
g. Factor out the common binomial: (2x + 5)(x – 3) // Factoring out the common binomial
Factored Expression: -2(2x + 5)(x – 3) // Final factored form
Original Expression: 3x² + 7x + 2 // Result of multiplying (x+2)(3x+1)
Step 1: Identify the trinomial to factor: 3x² + 7x + 2 // Trinomial to factor
Step 2: Apply the AC method:
a. Multiply a and c in the trinomial ax² + bx + c: 3 * 2 = 6 // Finding the product ac
b. Find two numbers whose product is ac (6) and sum is b (7): 1 and 6 // Finding the numbers
c. Split the middle term using the numbers: 3x² + x + 6x + 2 // Splitting the middle term
d. Group the terms: (3x² + x) + (6x + 2) // Grouping the terms
e. Factor out the GCF from each group: x(3x + 1) + 2(3x + 1) // Factoring the groups
f. Factor out the common binomial: (x + 2)(3x + 1) // Factoring out the common binomial
Factored Expression: (x + 2)(3x + 1) // Final factored form
Original Expression: 12x² + x – 1 // Result of multiplying (4x+1)(3x-1)
Step 1: Identify the trinomial to factor: 12x² + x – 1 // Trinomial to factor
Step 2: Apply the AC method:
a. Multiply a and c in the trinomial ax² + bx + c: 12 * (-1) = -12 // Finding the product ac
b. Find two numbers whose product is ac (-12) and sum is b (1): 4 and -3 // Finding the numbers
c. Split the middle term using the numbers: 12x² + 4x – 3x – 1 // Splitting the middle term
d. Group the terms: (12x² + 4x) + (-3x – 1) // Grouping the terms
e. Factor out the GCF from each group: 4x(3x + 1) – 1(3x + 1) // Factoring the groups
f. Factor out the common binomial: (4x + 1)(3x – 1) // Factoring out the common binomial
Factored Expression: (4x + 1)(3x – 1) // Final factored form