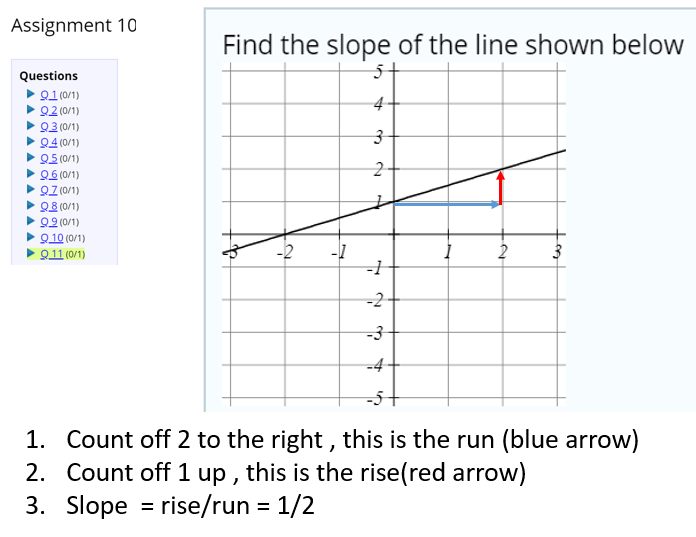
Finding the Slope of a Linear Function from a Graph
| Mathematical Steps | Explanation |
|---|---|
| Identify Two Points | Pick two distinct points on the line in the graph. The more accurate these points are, the more accurate your slope calculation will be. |
| Note the Coordinates | Write down the coordinates of these two points. Let the coordinates of the first point be (x₁, y₁) and the second point be (x₂, y₂). |
| Calculate Δy = y₂ – y₁ | Subtract the y-coordinate of the first point from the y-coordinate of the second point to find the change in y, denoted as Δy. |
| Calculate Δx = x₂ – x₁ | Subtract the x-coordinate of the first point from the x-coordinate of the second point to find the change in x, denoted as Δx. |
| Calculate Slope (m) = Δy / Δx | Divide the change in y by the change in x to find the slope. The formula for slope is m = Δy / Δx. |
| Interpret the Slope | The slope tells you how steep the line is. A positive slope means the line rises as you move from left to right. A negative slope means it falls. A zero slope means the line is horizontal, and an undefined slope means the line is vertical. |
Final Thoughts
By following these steps, you can easily find the slope of a linear function from a graph. The slope is a crucial element in understanding the behavior of the line.