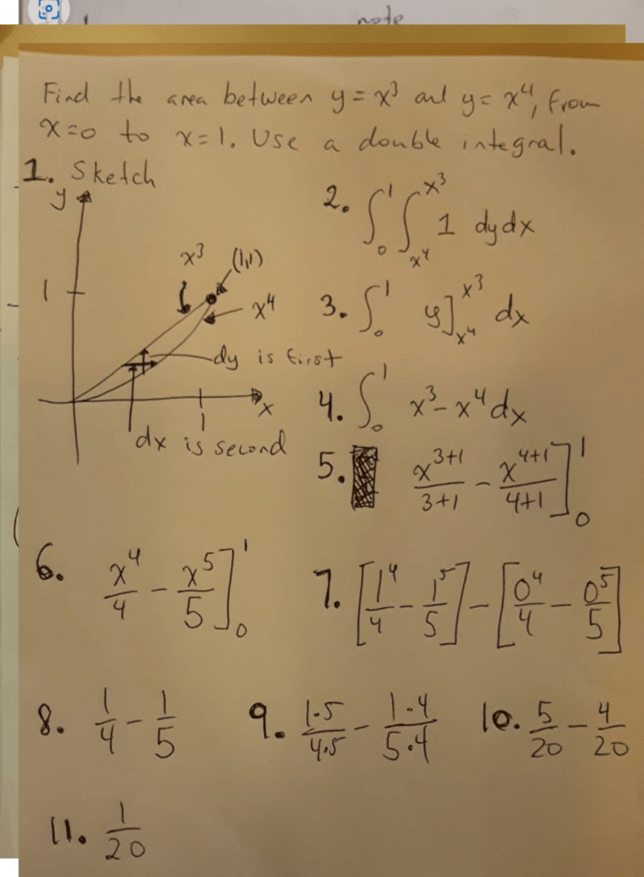
Original Question: Find the area between \( y = x^3 \) and \( y = x^4 \) from \( x = 0 \) to \( x = 1 \) using a double integral.

Step 1:

\[ \int \int dy \, dx \]

We start with the general form of a double integral. This sets the stage for integrating first with respect to \(y\) and then \(x\).

Step 2:

\[ \int_{0}^{1} \int dy \, dx \]

Next, we specify the limits for \(x\), which go from 0 to 1 as given in the problem.

Step 3:

\[ \int_{0}^{1} \int_{x^4}^{x^3} 1 \, dy \, dx \]

The integrand is 1 because we are finding the area between the curves. The area of a differential element \(dy \, dx\) is simply 1.

Step 4:

\[ \int_{0}^{1} \int_{x^4}^{x^3} dy \, dx \]

Now we set the limits for \(y\), which are determined by the equations \(y = x^3\) and \(y = x^4\).

Step 5:

\[ \int_{0}^{1} (x^3 – x^4) \, dx \]

We simplify the inner integral by subtracting the lower \(y\)-limit from the upper \(y\)-limit, resulting in \(x^3 – x^4\).

Step 6:

\[ \int_{0}^{1} x^3 \, dx – \int_{0}^{1} x^4 \, dx \]

We can separate this into two integrals for easier calculation.

Step 7:

\[ \left[\frac{x^4}{4}\right]_{0}^{1} \]

The integral of \(x^3\) is \(\frac{x^4}{4}\), and we evaluate this from 0 to 1.

Step 8:

\[ \left[\frac{x^5}{5}\right]_{0}^{1} \]

The integral of \(x^4\) is \(\frac{x^5}{5}\), and we also evaluate this from 0 to 1.

Step 9:

\[ \frac{1}{4} – \frac{1}{5} \]

We subtract the two results to get the final area between the curves.

Step 10:

\[ \frac{1}{4} – \frac{1}{5} = \frac{5}{20} – \frac{4}{20} = \frac{1}{20} \]

To find the numerical value of the area, we find a common denominator for the fractions, which is 20. After performing the subtraction, we get \( \frac{1}{20} \) as the final area between the curves.

Graphing the Area Between \(y = x^3\) and \(y = x^4\)

This guide explains how to graphically represent the area between \(y = x^3\) and \(y = x^4\) from \(x = 0\) to \(x = 1\), which we previously calculated to be \( \frac{1}{20} \) using a double integral.

Step 1: Set Up the Coordinate Plane

Draw the x-axis and y-axis. Label the x-axis from 0 to 1 and the y-axis according to the range of the functions.

Step 2: Plot \(y = x^3\)

Start at the origin and plot points for \(x\) between 0 and 1. Connect the points to form the curve.

Step 3: Plot \(y = x^4\)

Similarly, start at the origin and plot points for \(x\) between 0 and 1. Connect these points to form the second curve.

Step 4: Identify Intersection Points

The curves intersect at \(x = 0\) and \(x = 1\).

Step 5: Shade the Area

Shade the area between the two curves from \(x = 0\) to \(x = 1\).

Step 6: Label the Graph

Label both curves, the x-axis, and y-axis. Indicate the points of intersection and the shaded area.

Step 7: Relate to Integral

The shaded area represents the value we calculated using a double integral, which is \( \frac{1}{20} \).