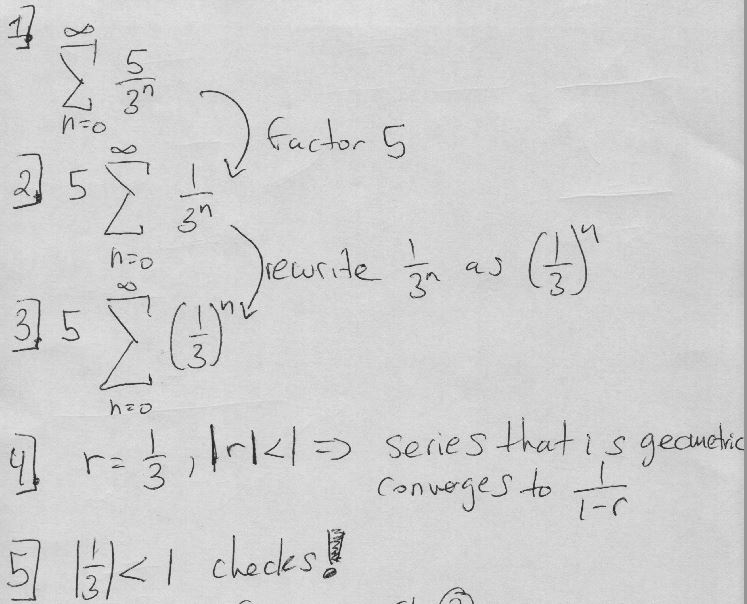
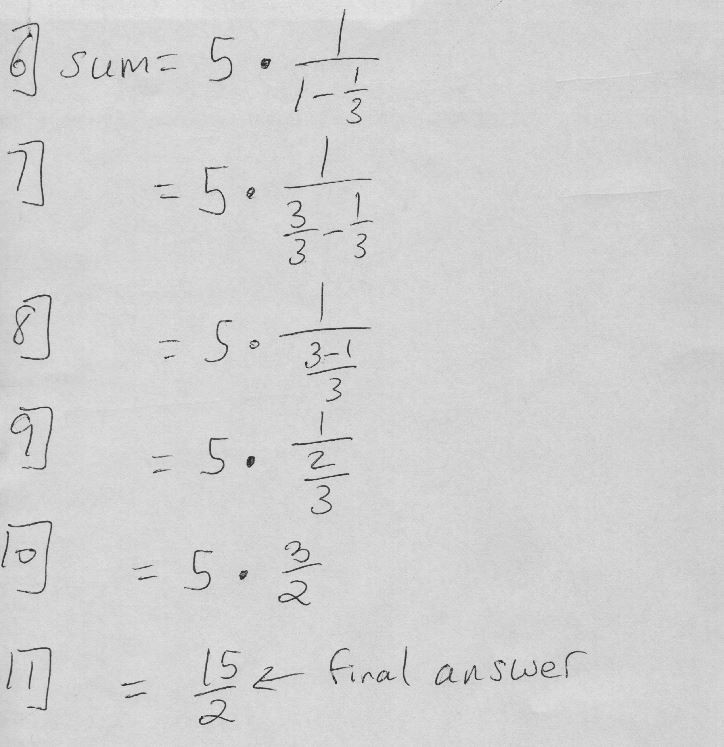
Convergence or Divergence of \(\sum_{n=0}^{\infty} \frac{5}{3^n}\)

This guide explains how to determine if the mathematical series \(\sum_{n=0}^{\infty} \frac{5}{3^n}\) converges or diverges using the formula for an infinite geometric series.

Step 1: Identify the Series Type

The series is a geometric series with \( a = 5 \) and \( r = \frac{1}{3} \).

Step 2: Check the Common Ratio

We need to check if the common ratio \( |r| < 1 \) for the series to converge.

Output: \( |r| = |\frac{1}{3}| = \frac{1}{3} < 1 \)

Step 3: Apply the Geometric Series Formula

Since \( |r| < 1 \), the series converges and its sum can be found using the formula \( S = \frac{a}{1 - r} \).

Output: \( S = \frac{5}{1 – \frac{1}{3}} = \frac{5}{\frac{2}{3}} = \frac{15}{2} = 7.5 \)

Conclusion

By using the formula for an infinite geometric series, we can conclude that the series \(\sum_{n=0}^{\infty} \frac{5}{3^n}\) converges and its sum is \( 7.5 \).