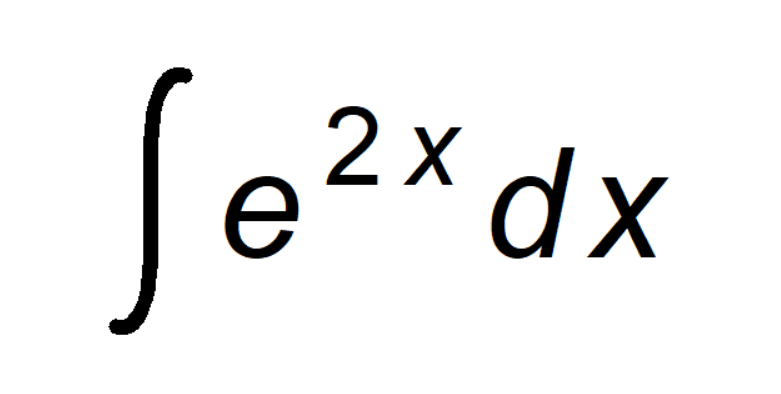1. Start with the integral you want to solve:

∫ e²ˣ dx

This represents the area under the curve of e²ˣ.

2. Make a substitution for the exponent, letting u = 2x:

∫ eᵘ · (du/2)

By letting u = 2x, we simplify the expression, and (du/2) accounts for the chain rule.

3. Integrate eᵘ with respect to u:

(1/2) ∫ eᵘ du = (1/2) eᵘ + C

The integral of eᵘ is simply eᵘ, and we multiply by (1/2) to account for the earlier substitution.

4. Substitute back for u:

(1/2) e²ˣ + C

Replacing u with 2x gives the final result.

So the integral of e²ˣ is (1/2) e²ˣ + C, where C is the constant of integration.