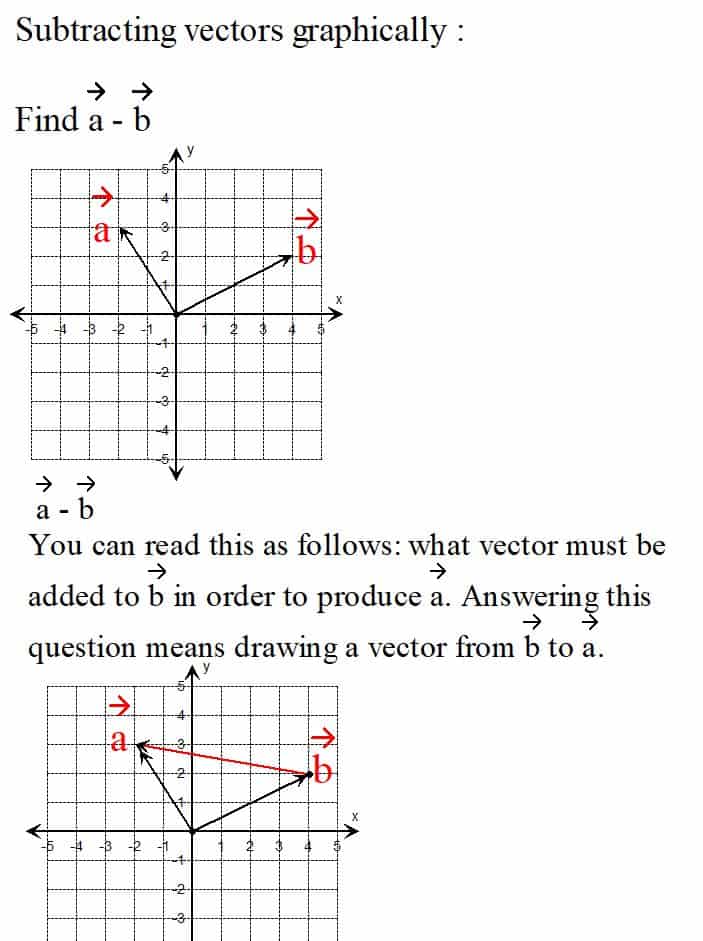
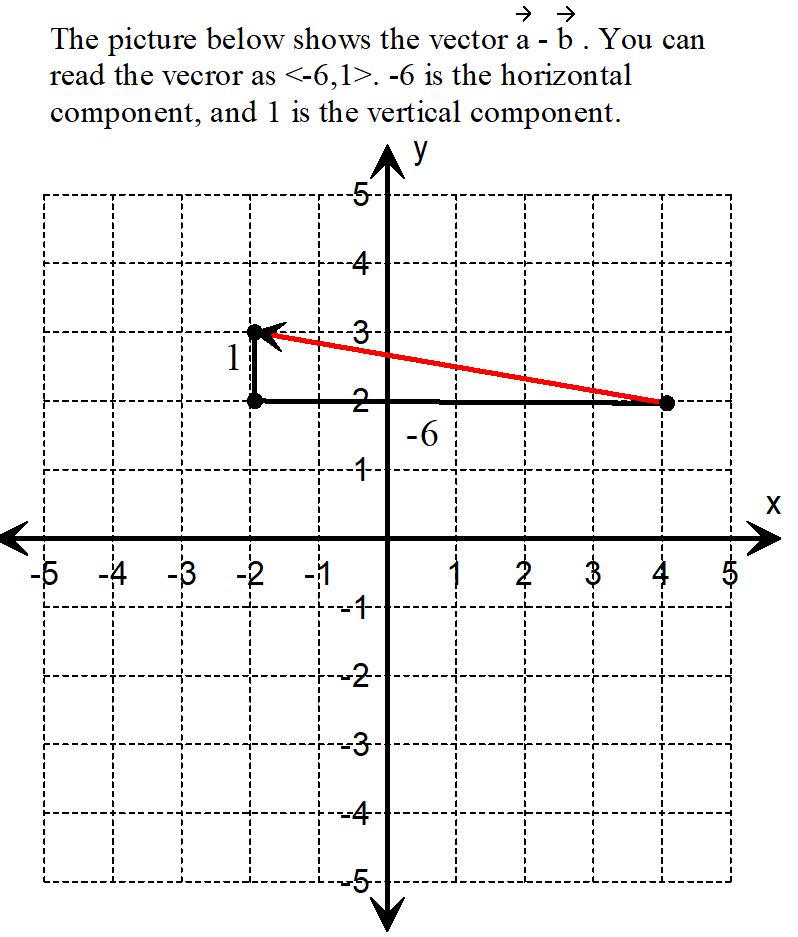
Subtracting Vectors Graphically: An Example

Let’s say you want to subtract vector \( \mathbf{b} = \langle 2,5 \rangle \) from another vector \( \mathbf{a} \). Here’s how to do it graphically:

1. Pick a Scale: Choose a scale, like 1 cm equals 1 unit.
2. Draw Vector \( \mathbf{a} \): Draw vector \( \mathbf{a} \) with its length and direction. Let’s say \( \mathbf{a} = \langle 4,3 \rangle \).
3. Reverse Vector \( \mathbf{b} \): Write down the opposite of vector \( \mathbf{b} \): \( -\mathbf{b} = \langle -2,-5 \rangle \).
4. Add Reversed Vector \( \mathbf{b} \): From the tip of vector \( \mathbf{a} \), draw the reversed vector \( \langle -2,-5 \rangle \).
5. Connect Start to Finish: Draw a line from the start of \( \mathbf{a} \) to the end of the reversed \( \mathbf{b} \). This new vector \( \mathbf{a} – \mathbf{b} = \langle 2,-2 \rangle \) is the difference.
6. Find the Difference: Measure the final vector using the scale. It represents the subtraction of \( \mathbf{b} \) from \( \mathbf{a} \).

Conclusion: By reversing the vector you want to subtract and then adding it to the original vector, you can visually find the difference. In this example, subtracting \( \langle 2,5 \rangle \) from \( \langle 4,3 \rangle \) gives \( \langle 2,-2 \rangle \). This method helps you see how vectors interact and provides a clear picture of the subtraction process.