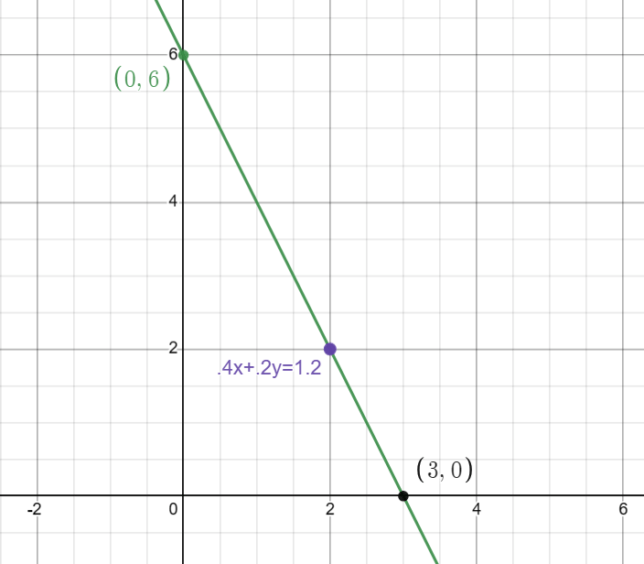Graphing a Line By X and Y Intercepts: Discover the process of graphing linear equations using x and y intercepts through our practical examples. Learn how to pinpoint where the line crosses the x and y axes by setting one variable to zero. Explore the connections between coefficients and intercepts in various equations, including whole numbers, decimals, and fractions. Whether dealing with straightforward equations or more intricate scenarios, master the essentials of graphing lines in the form ax + by = c with simplicity.

Finding the x-intercept:

2x + 3(0) = 6 ; Set y = 0 in the equation
2x = 6 ; Simplify by multiplying 3 by 0
x = 3 ; Divide by 2 to solve for x
So the x-intercept is at the point (3, 0).

Finding the y-intercept:

2(0) + 3y = 6 ; Set x = 0 in the equation
3y = 6 ; Simplify by multiplying 2 by 0
y = 2 ; Divide by 3 to solve for y
So the y-intercept is at the point (0, 2).

Graphing the Equation:

Graph of 2x + 3y = 6

Graphing a Line By X and Y Intercepts

Finding the x-intercept:

4x – 2(0) = 8 ; Set y = 0 in the equation
4x = 8 ; Simplify by multiplying -2 by 0
x = 2 ; Divide by 4 to solve for x
So the x-intercept is at the point (2, 0).

Finding the y-intercept:

4(0) – 2y = 8 ; Set x = 0 in the equation
-2y = 8 ; Simplify by multiplying 4 by 0
y = -4 ; Divide by -2 to solve for y
So the y-intercept is at the point (0, -4).

Graphing the Equation:

Graph of 4x - 2y = 8

Graphing a Line By X and Y Intercepts

Finding the x-intercept:

5x + 3(0) = 15 ; Set y = 0 in the equation
5x = 15 ; Simplify by multiplying 3 by 0
x = 3 ; Divide by 5 to solve for x
So the x-intercept is at the point (3, 0).

Finding the y-intercept:

5(0) + 3y = 15 ; Set x = 0 in the equation
3y = 15 ; Simplify by multiplying 5 by 0
y = 5 ; Divide by 3 to solve for y
So the y-intercept is at the point (0, 5).

Graphing the Equation:

Graph of 5x + 3y = 15

Graphing a Line By X and Y Intercepts

Finding the x-intercept:

\(\frac{1}{2}x – \frac{1}{3}(0) = \frac{1}{6}\) ; Set y = 0 in the equation
\(\frac{1}{2}x = \frac{1}{6}\) ; Simplify by multiplying -1/3 by 0
\(x = \frac{1}{3}\) ; Multiply by 2 to solve for x
So the x-intercept is at the point \(\left(\frac{1}{3}, 0\right)\).

Finding the y-intercept:

\(\frac{1}{2}(0) – \frac{1}{3}y = \frac{1}{6}\) ; Set x = 0 in the equation
\(-\frac{1}{3}y = \frac{1}{6}\) ; Simplify by multiplying 1/2 by 0
\(y = -\frac{1}{2}\) ; Multiply by -3 to solve for y
So the y-intercept is at the point \(\left(0, -\frac{1}{2}\right)\).

Description of the Graph:

The graph of the equation \(\frac{1}{2}x – \frac{1}{3}y = \frac{1}{6}\) is a straight line that passes through the x-intercept at \(\left(\frac{1}{3}, 0\right)\) and the y-intercept at \(\left(0, -\frac{1}{2}\right)\). By connecting these two points with a straight line, you can visualize the graph of the equation.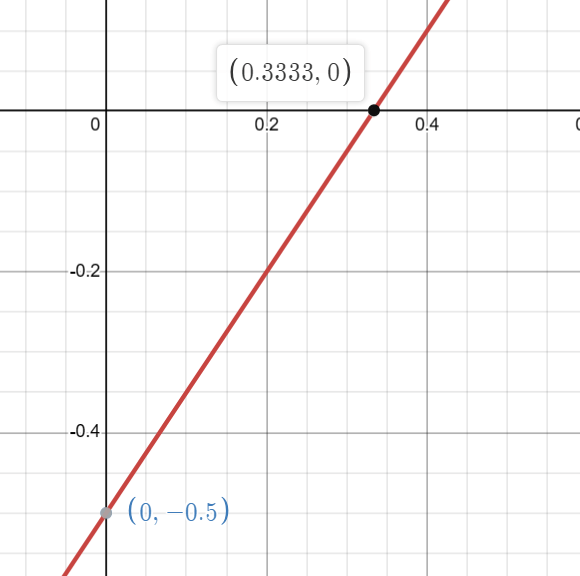

Graphing a Line By X and Y Intercepts

Original Equation:

\(0.4x + 0.2y = 1.2\)

Finding the x-intercept:

\(0.4x + 0.2(0) = 1.2\) ; Set y = 0 in the equation
\(0.4x = 1.2\) ; Simplify by multiplying 0.2 by 0
\(x = 3\) ; Divide by 0.4 to solve for x
So the x-intercept is at the point \((3, 0)\).

Finding the y-intercept:

\(0.4(0) + 0.2y = 1.2\) ; Set x = 0 in the equation
\(0.2y = 1.2\) ; Simplify by multiplying 0.4 by 0
\(y = 6\) ; Divide by 0.2 to solve for y
So the y-intercept is at the point \((0, 6)\).

Description of the Graph:

The graph of the equation \(0.4x + 0.2y = 1.2\) is a straight line that passes through the x-intercept at \((3, 0)\) and the y-intercept at \((0, 6)\). By connecting these two points with a straight line, you can visualize the graph of the equation.