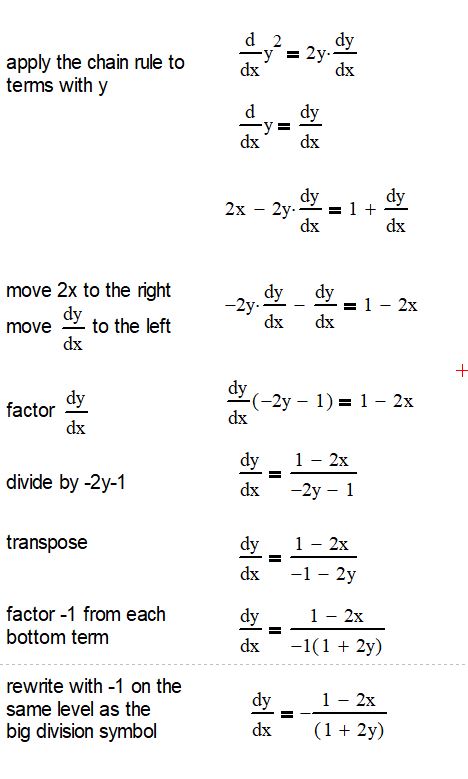
Implicit Derivative of x² – y² = x + y for Beginners

Mathematical Steps	Plain English Explanation
Start with the equation x² – y² = x + y	We have an equation that involves both x and y. We want to find out how y changes as x changes, but y isn’t isolated in the equation.
Differentiate both sides	To find out how y changes with respect to x, we need to take the derivative of both sides of the equation. This involves a bit of calculus.
Left Side: 2x – 2y(dy/dx)	The derivative of x² is 2x and the derivative of y² is 2y. But since y is also a function of x, we multiply the derivative of y² by dy/dx.
Right Side: 1 + dy/dx	The derivative of x is 1 and the derivative of y is dy/dx. We add these together.
Set them equal: 2x – 2y(dy/dx) = 1 + dy/dx	Now we set the derivatives from both sides equal to each other. This gives us a new equation to solve.
Isolate dy/dx: dy/dx = (1 – 2x) / (2y – 1)	We rearrange the equation to solve for dy/dx, which tells us how y changes as x changes.

Final Result

The way y changes with respect to x, also known as dy/dx, for the equation x² – y² = x + y is (1 – 2x) / (2y – 1).