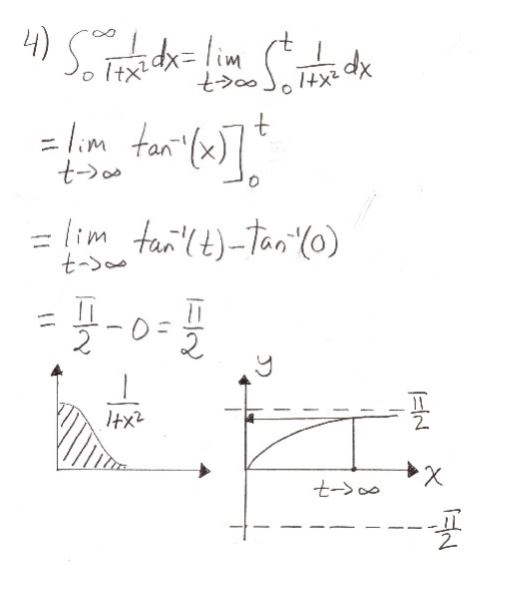
Understanding the Improper Integral of \( \frac{1}{1 + x^2} \) from 0 to Infinity

If you’ve ever wondered how mathematics can be used to deal with “infinity,” you’re in the right place. In this detailed guide, we’re tackling an integral that takes on the intimidating task of summing up an infinite number of terms. Specifically, we’re looking at the integral \( \int_{0}^{\infty} \frac{1}{1 + x^2} \, dx \). But don’t worry, even if you’re new to this, we’re breaking it down step by step.

Why Should You Care?

Now, you may be asking, why should I even care about this specific integral? Well, integrals like this one are fundamental in several areas of science and engineering, from physics to economics. They also serve as valuable exercises in understanding the concept of “infinity” in mathematics.

Step 1: The Challenge of Infinity

When it comes to infinity, regular methods for solving integrals can’t be directly applied. Therefore, we need to convert our “improper” integral into a more “proper” form that we can manage. We do this by introducing a variable \( b \) and taking its limit as it approaches infinity.

\[ \lim_{{b \to \infty}} \int_{{0}}^{{b}} \frac{1}{1 + x^2} \, dx \]

Step 2: What’s an Antiderivative?

The antiderivative is essentially the reverse of a derivative. It’s the function that, when differentiated, gives back the function we started with. For our function \( \frac{1}{1 + x^2} \), the antiderivative is \( \arctan(x) \).

\[ \arctan(x) + C \]

Step 3: Inserting the Boundaries

Now, let’s apply the lower and upper boundaries \( 0 \) and \( b \) into the antiderivative. This step allows us to get a concrete number to work with.

\[ \arctan(b) – \arctan(0) = \arctan(b) \]

Step 4: Back to Infinity (Sort Of)

The next phase involves us looking at what happens to our number when \( b \) approaches infinity. In simpler terms, we’re now going to see what happens when we try to go on forever.

\[ \lim_{{b \to \infty}} \arctan(b) \]

Step 5: Does It Converge?

“Converge” is a fancy term for asking if our sequence of numbers reaches a stable, finite value as it approaches infinity. Here, \( \arctan(b) \) converges to \( \frac{\pi}{2} \) as \( b \) approaches infinity.

Conclusion: What Does It All Mean?

The improper integral \( \int_{0}^{\infty} \frac{1}{1 + x^2} \, dx \) turns out to converge to \( \frac{\pi}{2} \). This result may seem abstract, but it’s fundamentally important. It shows that even when dealing with infinite sums, mathematics provides the tools to arrive at a concrete, understandable result.

So, What’s Next?

If you’ve followed along until here, congratulations! You’ve just gotten a glimpse into the intriguing world of calculus and how it grapples with infinity. This is just the tip of the iceberg. There’s a lot more to explore, from the mysteries of other improper integrals to applications in real-world problems. So, keep questioning and keep learning!