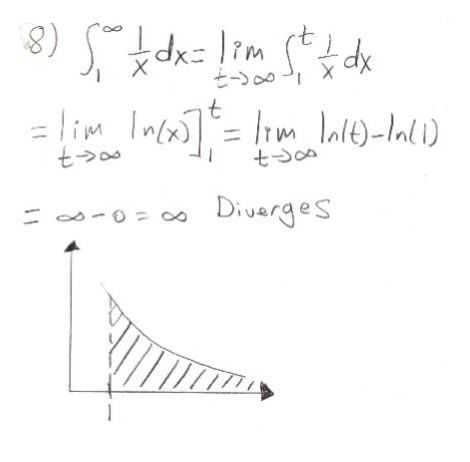
Step 1: Identifying the Function for Integration

We start by identifying the function we aim to integrate, which is \( \frac{1}{x} \). This function is a simple rational function with a single term in the denominator.

Step 2: Setting Up the Integral

We set up the integral with the given limits, which are \( x = 1 \) and \( x = \infty \):

\[ \int_{1}^{\infty} \frac{1}{x} \, dx \]

Step 3: Applying Limits for the Improper Integral

Since the integral has an infinite upper limit, it is an improper integral. We use limits to evaluate it:

\[ \lim_{{b \to \infty}} \int_{1}^{b} \frac{1}{x} \, dx \]

Step 4: Finding the Antiderivative

The antiderivative of \( \frac{1}{x} \) is \( \ln|x| + C \), where \( C \) is the constant of integration.

Step 5: Applying the Upper and Lower Limits

We apply the upper and lower limits to the antiderivative:

\[ [\ln|x|]_{1}^{b} \]

Step 6: Evaluating the Limits

After applying the limits, we find:

\[ \lim_{{b \to \infty}} (\ln|b| – \ln|1|) = \infty – 0 = \infty \]

Step 7: Final Result and Interpretation

The integral diverges, meaning it does not converge to a finite value. This result is intriguing because it shows that even a simple function like \( \frac{1}{x} \) can have an integral that diverges when evaluated over an infinite range.