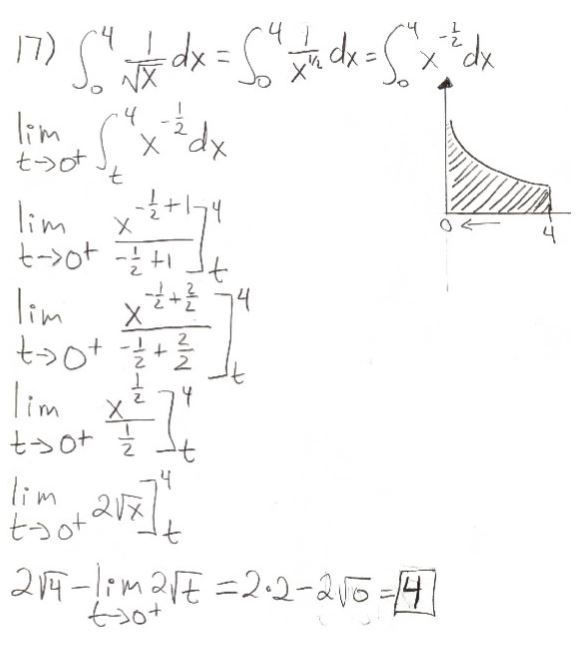
Calculation of Integral: \( \int_{0}^{4} \frac{1}{\sqrt{x}} \, dx \)

Let’s delve into the step-by-step construction of the definite integral \( \int_{0}^{4} \frac{1}{\sqrt{x}} \, dx \) and explore the reasoning behind each mathematical transformation.

Step 1: Evaluating the Indefinite Integral

We initiate our journey by finding the indefinite integral of \( \frac{1}{\sqrt{x}} \) with respect to \( x \):

\[ \int \frac{1}{\sqrt{x}} \, dx = 2\sqrt{x} + C \]

Here, the \( + C \) term symbolizes the constant of integration, which accounts for the family of curves that arise due to indefinite integration.

Step 2: Applying the Fundamental Theorem of Calculus

The fundamental theorem of calculus enables us to evaluate the definite integral by subtracting the antiderivative values at the upper and lower limits of integration:

\[ \int_{0}^{4} \frac{1}{\sqrt{x}} \, dx = \left(2\sqrt{4}\right) – \left(2\sqrt{0}\right) \]

\[ = 4 – 0 = 4 \]

As \( x \) varies from \( 0 \) to \( 4 \), the integral yields the finite result of \( 4 \).

Result: Finite Integral

The culmination of our mathematical exploration yields the following outcome:

\[ \int_{0}^{4} \frac{1}{\sqrt{x}} \, dx = 4 \]

This result signifies the finite area under the curve of \( \frac{1}{\sqrt{x}} \) from \( x = 0 \) to \( x = 4 \).

Unlike the previous case, where the integral was divergent, the finite interval of integration from \( 0 \) to \( 4 \) leads to a bounded area under the curve.