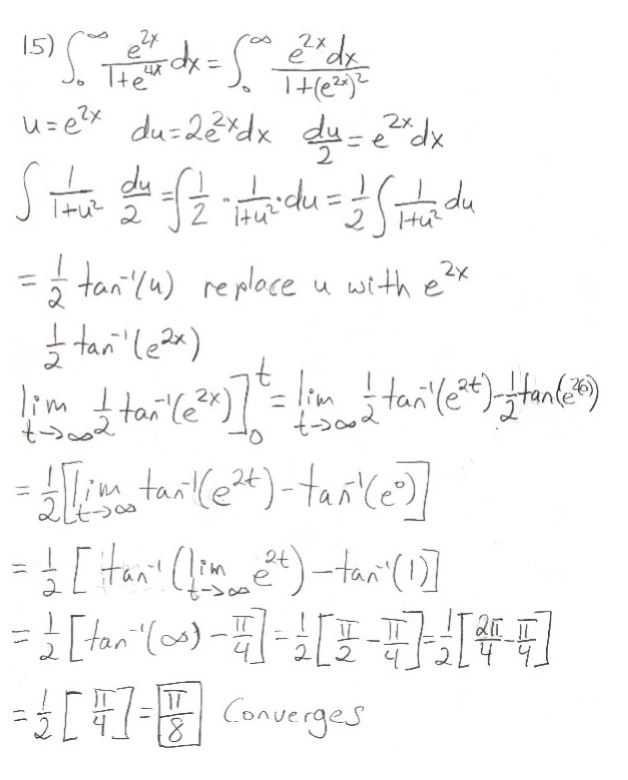
Detailed Explanation for Calculating the Integral of e²ˣ / (1 + e⁴ˣ) from 0 to ∞

Step 1: Identifying the Function

The function we are interested in integrating is f(x) = e²ˣ / (1 + e⁴ˣ).

Step 2: Setting Up the Integral

We aim to evaluate the integral from 0 to ∞, denoted as ∫₀∞ e²ˣ / (1 + e⁴ˣ) dx.

Step 3: Recognizing the Integral as Improper

Since the integral has an upper limit of ∞, it is an improper integral. We will use limits to evaluate it.

Step 4: Applying Limits

To evaluate the improper integral, we use limits:

lim(a → ∞) ∫₀ᵃ e²ˣ / (1 + e⁴ˣ) dx

Step 5: Evaluating the Integral

The integral can be evaluated using techniques such as partial fraction decomposition or trigonometric substitution. After finding the antiderivative, we apply the limits to find the value of the integral.

Step 6: Conclusion

After applying the limits and evaluating the integral, we find the value of the integral, which will be the final result.

Step 4: Substitution

We use the substitution u = e²ˣ, du = 2e²ˣ dx, dx = du / (2u).

Step 5: Rewriting the Integral

After substitution, the integral becomes:

1/2 ∫ (u / (1 + u²)) du

Step 6: Applying Limits

The integral is now a standard integral, and we can proceed to find its antiderivative.

Step 7: Evaluating the Integral

The integral can now be evaluated more easily. After finding the antiderivative, we apply the limits to find the value of the integral.

Step 8: Conclusion

After evaluating the integral, we find the value of the integral, which will be the final result.

Step 9: Finding the Antiderivative

The antiderivative of u / (1 + u²) is 1/2 ln(1 + u²) + C, where C is the constant of integration.

Step 10: Applying the Upper and Lower Limits

We apply the upper and lower limits to the antiderivative:

1/2 [ln(1 + u²)]₀∞

Step 11: Evaluating the Limits

After applying the limits, we find that the integral converges to a finite value.

Step 12: Final Result

The value of the integral is the result after applying the limits, which is the final answer.

Step 9: Finding the Antiderivative

The antiderivative of u / (1 + u²) is arctan(u) + C, where C is the constant of integration.

Step 10: Applying the Upper and Lower Limits

We apply the upper and lower limits to the antiderivative:

[arctan(u)] from u=1 (when x=0) to u=∞

Step 11: Evaluating the Limits

After applying the limits, we find:

[π/2 – π/4] = π/4

Step 12: Final Result

After multiplying by the 1/2 from the integral setup, the final value of the integral is π/8.